anthesco
- 3
- 0
Homework Statement
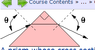
This is one of my homework questions. I think I have the right answer, but I don't understand how to figure out the "given" angle, so if someone could explain it to me, that would be great! Be sure to look at the picture attached...it's what's tricking me.
A prism whose cross section is shaped like an isosceles right triangle is made from a material with index of refraction, n = 1.31. Find the angle θ of the entering/exiting rays that travel parallel to the lower side (in degrees).
Homework Equations
Snell's law, n1*sin\theta1=n2*sin\theta2
The Attempt at a Solution
n1=1.31
n2=1
\theta1=45°
1.31*sin\theta1=1*sin\theta2
\theta2=67.867
What I need to know is how to figure out that the first angle is 45°.
Attachments
Last edited: