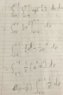Tom31415926535
- 9
- 0
Homework Statement
Let D be the triangle with vertices (0,0), (1,0) and (0,1). Evaluate:
∫∫exp((y-x)/(y+x))dxdy for D
by making the substitutions u=y-x and v=y+x
Homework Equations
The Attempt at a Solution
So first I found an equation for y and x respectively:
y=(u+v)/2 and x=(v-u)/2
Then I found the Jacobian of this transformation to be 1.
Then I started solving using the terminals as:
-v<u<v and 0<v<1
However, the final solution that I got is undefined (however I can see I was on the right track. The only issue is that there was a log(0) that screwed things up)
Where have I gone wrong?
The correct answer is 1/4(e-1/e)