- 2,076
- 140
Hi everyone.
I've been curious about a particular symbol, but I've never seen it used or mentioned in any context. I don't really have much information about its usage, so I thought I would ask around and see if anyone knew about its application.
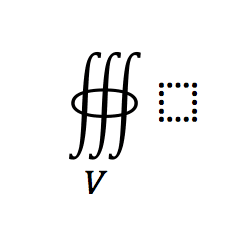
I saw this symbol in Microsoft word.
How do we interpret it, and how do we use it?
I'm familiar with closed surface integrals with differential elements ##d \vec S##. We use those when we want to calculate the flux of a field ##\vec F##. I'm also familiar with closed surface integrals with differential elements ##dS##. We use those when we want to calculate surface area.
What about the closed volume integral above though?
I know we should probably use a differential element ##dV## for a closed volume, and the answer would represent the volume of the object. Is there such thing as a differential volume element ##d \vec V## such that we can extend theorems to the fourth dimension (theorem's like Stoke's theorem and the Divergence theorem)?
Thank you in advance.
I've been curious about a particular symbol, but I've never seen it used or mentioned in any context. I don't really have much information about its usage, so I thought I would ask around and see if anyone knew about its application.
I saw this symbol in Microsoft word.
How do we interpret it, and how do we use it?
I'm familiar with closed surface integrals with differential elements ##d \vec S##. We use those when we want to calculate the flux of a field ##\vec F##. I'm also familiar with closed surface integrals with differential elements ##dS##. We use those when we want to calculate surface area.
What about the closed volume integral above though?
I know we should probably use a differential element ##dV## for a closed volume, and the answer would represent the volume of the object. Is there such thing as a differential volume element ##d \vec V## such that we can extend theorems to the fourth dimension (theorem's like Stoke's theorem and the Divergence theorem)?
Thank you in advance.