ChessEnthusiast
- 115
- 3
I've been wondering how I can find the pressure water exerts on a sphere it's in.
As for cyllinders and pyramids, and prisms - the thing is extremely easy - you just take the one formula and put in numbers.
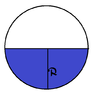
What about a situation when we have a sphere whose radius is R, and it's half full with water.
Could you explain to me in simple terms how to find this pressure?
If it's not possible to explain it in an easy way, then please use calculus.
As for cyllinders and pyramids, and prisms - the thing is extremely easy - you just take the one formula and put in numbers.
What about a situation when we have a sphere whose radius is R, and it's half full with water.
Could you explain to me in simple terms how to find this pressure?
If it's not possible to explain it in an easy way, then please use calculus.