What are the Correct Bounds for a Triple Integral with Symmetry?

[Poopsilon]

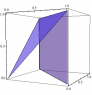
I'm trying to set up this triple integral with the following bounds: x=0, y=0, z=0, x+y=1, z=x+y.

Now I first computed the volume to be 1/3 with a double integral and then what I've been doing is setting what I think are the right bounds for the triple integral and integrating f(x,y,z)=1 to see if that matches the volume. I also think that because of symmetry ∫∫∫xdxdydz = ∫∫∫ydxdydz so I have been checking the correctness of my bounds that way as well.

Finally I have come up with bounds that check out both ways but they seem too simple to be correct, if you could help verify them or provide the correct ones if they are wrong that would be excellent.

Here they are from outer to inner: z=0 to z=1, y=0 to y=z, x=0 to x=z. Thanks.

 

[vela]

Those limits are not correct. I've attached a plot of the two planes, with z being the vertical axis. That should help you see what the limits should be.

 

[Poopsilon]

Ok so these are the bounds that make the most sense to me, outer to inner: z=0 to z=1, y=z to y=1, x=z-y to x=1-y. Now I actually had these bounds originally and the volume of the solid checks out with these bounds but I get different four dimensional volumes when I integrate f(x,y,z)=x and f(x,y,z)=y. So either my bounds are still wrong or my theory that due to symmetry these two triple integrals are equal is wrong.

 

[vela]

Those aren't correct either. If you project the volume onto the yz-plane, you'll see it's covers the square [0,1]x[0,1], so the limits of y should also be from 0 to 1.

 

[Poopsilon]

I'm sorry to bother you again but I simply cannot get this integral to work out, I now have the bounds from outer to inner at: z=0 to z=1, y=0 to y=1, and x=z-y to x=1-y.

Not only do these bounds not produce the same 4-D volume for f(x,y,z)=x and f(x,y,z)=y but when I check the volume of the domain with: ∫∫(x+y)dxdy = ∫∫∫dxdydz, I am getting 1/3 = 1/2. I am thoroughly flummoxed, could you at least tell me if the two different ways I'm trying to verify my answer are correct? Or are my bounds still wrong? Thanks.

 

[vela]

Your sanity checks are correct, and your bounds are still wrong. Here's another plot of the two planes except with the axes rotates so that the yz-plane is on the bottom. The limits for the x integrals should correspond to where a vertical line intersects the surface of the volume. Depending on where you are in the yz-plane, the limits for x are different.

 

[Poopsilon]

So are you implying that I need to break up my integral into two separate integrals if I iterate the integral in the order of dxdydz?

 

[vela]

Exactly.