- #1
Mastermind01
- 203
- 51
Homework Statement
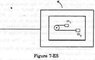
A table with smooth horizontal surface is placed in a cabin which moves in a circle of a large radius R (figure attached). A smooth pulley of small radius is fastened to the table. Two masses m and 2m placed on the table are connected through a string going over the pulley Initially the masses are held by a person with the strings" along the outward radius and then the system is released from rest (with respect to the cabin). Find the magnitude of the initial acceleration of the masses as seen from the cabin and the tension in the string.
Homework Equations
centripetal acceleration = [tex] \frac{v^2}{r } = \omega^2r [/tex]
The Attempt at a Solution
Assuming an acceleration of a of one of the masses attached to the pulley produces the two equations:
[tex] T = m(\omega^2R + a) [/tex]
and
[tex] T = 2m(\omega^2R - a) [/tex]
which solves the question and gives the requisite answer.
However my question is what causes the acceleration 'a' in the first place ? The only force acting on the masses is the tension 'T' which I think is the cause of the centripetal force.
Thanks.