What force is preventing car wheel bolts from being removed?

[ChessEnthusiast]

Let's say we want to change a wheel in a car. We want to remove bolts fastening the wheel using this tool:

I have also drawn a diagram of the forces in operation:

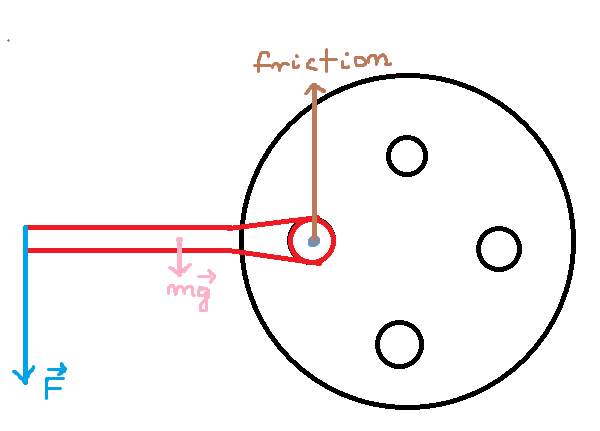
Now, from experience I can say that the point of rotation of the wrench will be the blue point. Now, trying to determine the torque relative to that point leaves us with a net torque anticlockwise (friction gets canceled out).

Yet, we know that removing these bolts requires some effort. Therefore, there either are more forces in action or the axis of rotation I chose is incorrect (or both)

What am I missing?

 

[A.T.]

Why is friction acting at the center of the bolt?

 

[Dale]

What am I missing?

There is a frictional torque as well as a frictional force.

 

[russ_watters]

No, there's no frictional force; friction applies the torque. The linear force shown on the diagram is applied by the bolt.

 

[A.T.]

No, there's no frictional force

What do you mean?

 

[ChessEnthusiast]

I see. So, to recap:
There are three forces acting on the wrench:

• gravity
• the force we apply
• the force the bolt applies

The last force does not contribute to the net torque. There are three factors contributing to it:

• gravity
• the force we apply
• the friction torque

Is it correct so far?

 

[Dullard]

1. Friction occurs at the threads of the nut/bolt, and on the mating face of the lug nut (not at the center of the bolt)
2. There is a 'normal' force perpendicular to the plane in your picture - it is the result of 'stretching' the stud and deforming the wheel/hub.

 

[russ_watters]

What do you mean?

Linear force. On a free body diagram you draw "forces" and "torques" (moments).

 

[Dale]

No, there's no frictional force; friction applies the torque. The linear force shown on the diagram is applied by the bolt.

Good catch! Yes, you are right. That is a normal force from the bolt, not a frictional force from the nut.

 

[A.T.]

Linear force. On a free body diagram you draw "forces" and "torques" (moments).

But there also are frictional forces at the thread of the bolt.

 

[russ_watters]

But there also are frictional forces at the thread of the bolt.

What do you mean?

 

[A.T.]

What do you mean?

The question is "What force is preventing car wheel bolts from being removed?" I'm picturing a threaded bolt screwed into the wheel. To get it out you need to overcome the static friction of the thread.

 

[russ_watters]

The question is "What force is preventing car wheel bolts from being removed?" I'm picturing a threaded bolt screwed into the wheel. To get it out you need to overcome the static friction of the thread.

Yes... It isn't clear to me why you think that contradicts what I said.

 

[jbriggs444]

Good catch! Yes, you are right. That is a normal force from the bolt, not a frictional force from the nut.

The situation between the nut and bolt is statically indeterminate. There is no way to tell whether normal force or frictional force is responsible for the net vertical force of bolt on nut.

 

[russ_watters]

The situation between the nut and bolt is statically indeterminate. There is no way to tell whether normal force or frictional force is responsible for the net vertical force of bolt on nut.

Good point. When tight, the friction between the face of the nut and wheel could be significant, if the nut is assumed to be flat...

...which they usually are not because you don't want friction supporting the wheel.

 

[Dale]

The situation between the nut and bolt is statically indeterminate. There is no way to tell whether normal force or frictional force is responsible for the net vertical force of bolt on nut.

Wow, this thread is full of great follow ups!

We would need something like a FEM to get the details, but overall there is a net force and a net torque

 

[A.T.]

Yes... It isn't clear to me why you think that contradicts what I said.

I was confused by your statement that "there's no frictional force". But we seem to agree that it's there now.

 

[sophiecentaur]

Good point. When tight, the friction between the face of the nut and wheel could be significant, if the nut is assumed to be flat...

...which they usually are not because you don't want friction supporting the wheel.

I'm not sure where this thread is going. Is there something that's not as obvious as it seems to me? An additional tangential force on the nut could have been added to the original diagram and that would have 'explained' everything, I think.

Screws and many other fasteners that do not involve 'riveting' of some sort remain in place due to friction. Without friction they would unscrew themselves and shelves would fall down. The pitch of the wheel nut thread is shallow and contributes to prevent movement of the nut around the stud when torqued up. Also, there is friction between the nut and the seating. Torque applied to tighten the nut causes tension in the stud which, in turn, produces more friction between the threads and under the nut face. The torque specification is there to prevent over stretching the stud. In some applications, bolts have to be replaced, once removed because the application requires the two faces to be held together with great force. (Some cylinder heads on IC engines.) Corrosion will increase the friction force after time and it can be high enough for the stud to shear before it shifts. The 50 ft lb for your average wheel nut should not be exceeded, even if one is feeling particularly fit.

If there is any slop of the wheel hole around the stud, and if the nut has a flat face friction is important or the wheel could move laterally to the stud and groove the thread. Wheel nuts are usually tapered and fit into a tapered dip in the wheel, to avoid this happening. (Just reinforcing / clarifying the point, Russ). This technique doesn't seem to be used in other applications; perhaps it's for the benefit of the non-engineering types who need a sloppy fit so that they can actually put a replacement wheel in place.

 

[russ_watters]

I'm not sure where this thread is going. Is there something that's not as obvious as it seems to me? An additional tangential force on the nut could have been added to the original diagram and that would have 'explained' everything, I think.

Much of the discussion has gone beyond what is shown in the diagram. But no, I would not add a "tangential force" on the nut, I'd add a torque. It's not applied at a single point, so it can't be drawn as being applied at a single point.

 

[CWatters]

The question is "What force is preventing car wheel bolts from being removed?" I'm picturing a threaded bolt screwed into the wheel. To get it out you need to overcome the static friction of the thread.

That force exists because the bolt is trying to rotate. It resists rotation so it's actually a torque.

 

[sophiecentaur]

Much of the discussion has gone beyond what is shown in the diagram. But no, I would not add a "tangential force" on the nut, I'd add a torque. It's not applied at a single point, so it can't be drawn as being applied at a single point.

You are right, strictly, but the tangential force would be an 'equivalent' force and would avoid mixing forces and torques in what should be a simple argument.

 

[russ_watters]

You are right, strictly, but the tangential force would be an 'equivalent' force and would avoid mixing forces and torques in what should be a simple argument.

Well, there's a couple of problems with that:
1. There's no distance specified, so we wouldn't know where to apply it.
2. It would need to be applied as two forces in opposite directions (a "couple") on opposite sides to avoid implying a new linear/normal force.

This is why I don't like calling or representing a torque as a "force", per my point to A.T.

 

[A.T.]

That force exists because the bolt is trying to rotate. It resists rotation so it's actually a torque.

The frictional forces create a torque. But they are still forces.

 

[A.T.]

But no, I would not add a "tangential force" on the nut, I'd add a torque. It's not applied at a single point, so it can't be drawn as being applied at a single point.

That makes perfect practical sense for the FBD. But if a question is explicitly about forces, I would still point to the frictional forces.

 

[russ_watters]

That makes perfect practical sense for the FBD. But if a question is explicitly about forces, I would still point to the frictional forces.

Fair enough, but we're here to answer the OP, aren't we? The OP gave a FBD(!) and even used the correct labels and language to describe it(!). I see no good reason to muddy the water by not addressing the OP's question as it is and identifying the answer for what it is.

Uncertainty about the source of the second force aside, the OP:
-Correctly identified the forces and where they act.
-Left out the [reaction] torque.

Evidently, you were not aware that it is common language to separate "forces" and "torques" and you prefer to call the torque a "force". Please just accept that you learned something and move on.

 

[Merlin3189]

Does anyone remember this recent thread? https://www.physicsforums.com/threads/answering-simple-questions.953955/

 

[russ_watters]

Does anyone remember this recent thread? https://www.physicsforums.com/threads/answering-simple-questions.953955/

It's an active topic of discussion in the moderator's forum.

 

[Nik_2213]

Slightly off topic but, given commercial tyre fitters often use pneumatic nut / bolt drivers for speed, you may find that wrench illustrated cannot shift nuts / bolts roadside. I've had cause to literally jump up and down on the supplied tool, whack it with a convenient brick, even stamp it to break the initial 'stiction'. For safety, such must be done before jacking vehicle...

After that, I got a neat telescopic wrench, and deploying its additional foot beat using mine...

FWIW, although it is a minor contribution at 'domestic' torque levels, there will be some stretching of the bolt within its thread, friction on the slightly distorted thread walls augmenting the resistance to rotation of the head tightened against the wheel etc. Industrially, bolts and studs may be torqued, pre-loaded to remarkable levels. A real Engineer could tell it better...

 

[jack action]

Now, from experience I can say that the point of rotation of the wrench will be the blue point. Now, trying to determine the torque relative to that point leaves us with a net torque anticlockwise (friction gets canceled out).

Yet, we know that removing these bolts requires some effort. Therefore, there either are more forces in action or the axis of rotation I chose is incorrect (or both)

What am I missing?

What you are missing is the concept of couple (which results in a torque). First, the force you call 'friction' is mislabeled. You should call it 'reaction force'. When you apply the force at the end of the lever (in addition to the force due gravity), you have a reaction force from the stud itself that is equal and opposite to the sum of those forces. You can see that by noticing that the tire will squeeze a little bit more because you are pushing down on it (If you were pulling the lever up, you might even lift up the wheel off the ground).

Because the forces are misaligned, they constitute a couple, which creates a torque (in this case, anticlockwise). You seem to think that because the forces are equal and opposite, they "absorb" each other and thus cannot contribute to the torque. That is not the case. In static (i.e. no motion), forces must be opposed by other forces and they all contribute to torque. If the sum of the torques they create is zero, then there is no resultant torque.

In the case you presented, you should add a clockwise torque on your diagram. This torque comes from the friction between the thread of the stud & nut and it will be equal and opposite to the torque created by the couples coming from the applied forces (your hand & part of the reaction force, and the force due to gravity & the rest of the reaction force).

 

[sophiecentaur]

Much of the discussion has gone beyond what is shown in the diagram. But no, I would not add a "tangential force" on the nut, I'd add a torque. It's not applied at a single point, so it can't be drawn as being applied at a single point.

I can't disagree but the concept of Moments is introduced in Science Education well before Torque. If you take moments about the axis of the stud, you can ignore any force on that reference point. As a starter, I would say that the idea of an 'equivalent' tangential force would be more than acceptable when discussing the action of a wrench with students up to A Level. I think we tend to forget just how elementary, elementary means.

 

[sophiecentaur]

commercial tyre fitters often use pneumatic nut / bolt drivers for speed,

They are required, in the UK, to use a calibrated torque wrench for the final tightening. I have seen this in practice for several years now (state of the roads is much worse these days). The instructions also forbid the use of grease on the mating faces.

 

[russ_watters]

I can't disagree but the concept of Moments is introduced in Science Education well before Torque.

Is it? I would think they would be taught on the same day. Is this before or after learning about "couples"? Anyway, even if that's true, this problem would be the perfect setting to introduce the concept of torque. And:

If you take moments about the axis of the stud, you can ignore any force on that reference point. As a starter, I would say that the idea of an 'equivalent' tangential force would be more than acceptable when discussing the action of a wrench with students up to A Level. I think we tend to forget just how elementary, elementary means.

What you're now suggesting is to teach an unnecessary and potentially harmful skill/concept - how to pull forces and levers out of thin air and apply them to a problem - in order to avoid teaching a necessary one. How is that not counterproductive?

...actually, double-checking the definitions, the difference between "torque" and "moment" is purely functional; torque is an in-motion moment, whereas moments can be static or in motion. So this objection about the order of teaching is moot.

 

[sophiecentaur]

I would think they would be taught on the same day. Is this before or after learning about "couples"?

I think we are talking about different levels of teaching. The definition and the 'principle' of Moments comes long before Couples. You may be thinking in terms of your own education, as someone (a minority) who tended to find that most of early Physics made sense to you. Levers are much easier appreciated than gears by most students (adults too),
PS levers and seesaws, where the forces are all parallel are about as far as many people go. The "Perpendicular Distance" is a taxing idea, even for some A level students.

 

[russ_watters]

I think we are talking about different levels of teaching. The definition and the 'principle' of Moments comes long before Couples.

That's a problem for your suggestion then, since your idea requires a couple.

 

[sophiecentaur]

That's a problem for your suggestion then, since your idea requires a couple.

But not Explicitly. The word Couple is not actually necessary. It's actually quite a bit more sophisticated compared with introducing a Fulcrum and taking moments about it (with parallel forces mostly). People very often miss the requirement for the fulcrum to be fixed - or they just assume they can ignore it. Strangely, I was never asked the question "What about the force on the fulcrum?" That was one reason for my present opinion.