lec0x
- 3
- 0
Force With Angles!
A child pulls a wagon with a force of 59 N by a handle making an angle of 20 degrees with the horizontal. If the wagon has a mass of 5.2 kg, to the nearest hundredth of a m/s2 what is the acceleration of the wagon?
ƩF=ma
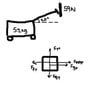
I drew a picture of the wagon and I know that if a child is exerting a force of 59N on the handle then the handle is exerting that back. does that mean that the handle is exerting that force onto the wagon as well?
The free body diagram has Force Normal going up, mgsin(θ) to the right as well as Force Applied, mgcos(θ) going down and Force friction going to the left!
ƩFy=ForceN-mgcos(θ)=0 so FN=mgcos(20)
and then ƩFx = Fpp+mgsin(20)-umgcos(20)
then would the force applied just be 59N or would there have to be an equation using θ
Homework Statement
A child pulls a wagon with a force of 59 N by a handle making an angle of 20 degrees with the horizontal. If the wagon has a mass of 5.2 kg, to the nearest hundredth of a m/s2 what is the acceleration of the wagon?
Homework Equations
ƩF=ma
The Attempt at a Solution
I drew a picture of the wagon and I know that if a child is exerting a force of 59N on the handle then the handle is exerting that back. does that mean that the handle is exerting that force onto the wagon as well?
The free body diagram has Force Normal going up, mgsin(θ) to the right as well as Force Applied, mgcos(θ) going down and Force friction going to the left!
ƩFy=ForceN-mgcos(θ)=0 so FN=mgcos(20)
and then ƩFx = Fpp+mgsin(20)-umgcos(20)
then would the force applied just be 59N or would there have to be an equation using θ
Attachments
Last edited: