What is the heat current in rod 1 and how can it be calculated?

In summary, the conversation discusses the heat current in a Y-shaped figure composed of three rods with identical properties. The free end of one rod is maintained at a higher temperature, while the free ends of the other two rods are maintained at a lower temperature. The conversation also mentions the junction temperature, T2, and provides equations for calculating the heat flow from T1 to T2 and T2 to T0. Ultimately, the conversation is seeking to solve for the heat current, H_1, in rod 1 using variables such as k, L, A, T_1, and T_0.
  • #1
jackson1984
1
0
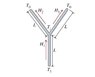
Three identical rods are welded together to form a Y-shaped figure. The cross-sectional area of each rod is A, and they have length L and thermal conductivity k.
The free end of rod 1 is maintained at T_1 and the free ends of rods 2 and 3 are maintained at a lower temperature T_0. You may assume that there is no heat loss from the surfaces of the rods.

What is the heat current H_1 in rod 1?
Express the heat current in terms of any or all of k, L, A, and the temperatures T_1 and T_0.

I guess the ans is (2kA/3L)(T_1+T_2), but it is wrong...
Can anyone teach me...
 

Attachments

  • 36907.jpg
    36907.jpg
    5.9 KB · Views: 627
Physics news on Phys.org
  • #2
What is your T2?

Anyway:
label the junction temperature as T2. Then write the heat flow equations for heat from T1 to T2 and T2 to T0. Solve for T2, then dQ/dt is obvious.
 

1. What is heat flow through three rods?

Heat flow through three rods is a process in which heat is transferred from one end of three connected rods to the other end. This process is governed by the laws of thermodynamics and can be studied using mathematical models and experiments.

2. How is heat flow through three rods calculated?

The rate of heat flow through three rods can be calculated using the equation Q/t = kA(T1-T2)/L, where Q is the amount of heat transferred, t is the time taken, k is the thermal conductivity, A is the cross-sectional area, T1 and T2 are the temperatures at the two ends of the rods, and L is the length of the rods.

3. What factors affect heat flow through three rods?

There are several factors that can affect heat flow through three rods, including the thermal conductivity of the rods, the temperature difference between the two ends, the cross-sectional area of the rods, and the length of the rods. Other factors such as the material of the rods and the presence of any insulating materials can also impact heat flow.

4. What are the applications of studying heat flow through three rods?

Studying heat flow through three rods has many practical applications, such as in the design of thermal insulation materials, heat transfer systems, and thermal management in various industries. It also helps in understanding the principles of heat transfer and developing more efficient and sustainable energy systems.

5. How can heat flow through three rods be manipulated?

The rate of heat flow through three rods can be manipulated by changing the factors that affect it, such as the thermal conductivity, temperature difference, and cross-sectional area of the rods. Insulating materials can also be used to reduce heat flow. Additionally, controlling the length and material of the rods can also impact heat flow.

Similar threads

I Calculation of temperature changes (heating a cube in a microwave oven)
    • Thermodynamics
Replies
9
Views
764
Heat Flow Through a Truncated Cone
    • Advanced Physics Homework Help
Replies
3
Views
3K
Electric heat generation from parallel rods carrying current in an oil bath
    • Introductory Physics Homework Help
Replies
11
Views
737
I How to measure average thermal conductivity of a metallic material?
    • Classical Physics
Replies
1
Views
525
How can vacuum heating be calculated for substrates in a chamber?
    • Mechanical Engineering
Replies
5
Views
1K
What is the temperature at the wire/insulator interface?
    • Advanced Physics Homework Help
Replies
8
Views
2K
How Does Thermal Conductivity Affect Heat Transfer Between Two Water Vessels?
    • Introductory Physics Homework Help
Replies
1
Views
911
What Is the Temperature Distribution Along an Insulated Rod?
    • Advanced Physics Homework Help
Replies
4
Views
2K
Heat gain (or Loss) in steady state from Metal Rod
    • General Engineering
Replies
1
Views
2K
Solve Heat Current Problem at Junction of Copper, Brass & Steel Rods
    • Advanced Physics Homework Help
Replies
1
Views
6K

Hot Threads

Recent Insights

Back
Top