What is the relationship between electric field and charge distribution?

[stunner5000pt]

pleas help! electric field

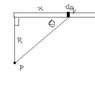
a semi infinite insulting rod carries a constant charge per unit length of lambda. SHow that he electric field at the point P makes an angle of 45 with the rod and that this result is independant of R

q = \lambda x
dq = \lambda dx

for the Y direction poiting downward
dE_{y} = \int_{0}^{\infty} \frac{1}{4 \pi \epsilon_{0}} \frac{\lambda dx}{R^2 + x^2} \sin{\theta}
\sin{\theta} = \frac{x}{R^2 + x^2}
dE_{y} = \int_{0}^{\infty} \frac{1}{4 \pi \epsilon_{0}} \frac{\lambda R dx}{(R^2 + x^2)^\frac{3}{2}}
dE_{y} = \frac{\lambda R}{4 \pi \epsilon_{0}} \int_{0}^{\infty} \frac{dx}{(R^2 + x^2)^\frac{3}{2}}
dE_{y} = \frac{\lambda R}{4 \pi \epsilon_{0}} [\frac{x}{R^2 \sqrt{R^2+x^2}}]_{0}^{\infty}
now I am not sure about this integral and whether or not it converges...

for the horizontal pointing left
\frac{\lambda R}{4 \pi \epsilon_{0}} \int_{0}^{\infty} \frac{xdx}{(R^2 + x^2)^\frac{3}{2}}
same problem here

please help!

 

[quasar987]

a semi infinite insulting rod carries a constant charge per unit length of lambda. SHow that he electric field at the point P makes an angle of 45 with the rod and that this result is independant of R

q = \lambda x
dq = \lambda dx

for the Y direction poiting downward
dE_{y} = \int_{0}^{\infty} \frac{1}{4 \pi \epsilon_{0}} \frac{\lambda dx}{R^2 + x^2} \sin{\theta}
\sin{\theta} = \frac{x}{R^2 + x^2}
dE_{y} = \int_{0}^{\infty} \frac{1}{4 \pi \epsilon_{0}} \frac{\lambda R dx}{(R^2 + x^2)^\frac{3}{2}}
dE_{y} = \frac{\lambda R}{4 \pi \epsilon_{0}} \int_{0}^{\infty} \frac{dx}{(R^2 + x^2)^\frac{3}{2}}
dE_{y} = \frac{\lambda R}{4 \pi \epsilon_{0}} [\frac{x}{R^2 \sqrt{R^2+x^2}}]_{0}^{\infty}
now I am not sure about this integral and whether or not it converges...

The integral is right and the limit to evaluate is almost trivial: pull x² out of the square root.

 

[stunner5000pt]

ok for the Y part
E_{y} = \frac{\lambda}{4 \pi \epsilon_{0}R}
i swhat i got the Y part. Am i right??

for the X part
i got the same thing.
However the resultant for these two given a 45 degree angle... however it isn ot independat of R as in
E = \sqrt{2} \frac{\lambda}{4 \pi \epsilon_{0}R}