What is the value of y in this water tank pressure problem?

[foo9008]

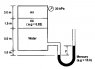
Homework Statement

i am asked to find the value of y in this question . I am not sure should i consider the atmospheric pressure acting on the mercury or not .

Homework Equations

The Attempt at a Solution

i choose to consider the atmospheric pressure as 0 in this case . So , my working is 30000 + (1.5x820x9.81) + (5 x1000x9.81) =13600(9.81)y , where y = 0.68m , am i right ? btw , i am not very sure about whether the pressure of water is (5 x1000x9.81) or not , because the outlet is not at bottom of teh tank , can someone exp;lain pls ?

 

[billy_joule]

If the pipe were even lower than the 1m shown (say 100m lower) would the pressure at the water-mercury interface be affected? So should you account for that 1m height by adding it to the 5m?

Wether you can ignore atmospheric pressure depends on if the pressure gauge is showing absolute pressure or pressure relative to atmospheric ('gauge' pressure).

 

[foo9008]

If the pipe were even lower than the 1m shown (say 100m lower) would the pressure at the water-mercury interface be affected? So should you account for that 1m height by adding it to the 5m?

Wether you can ignore atmospheric pressure depends on if the pressure gauge is showing absolute pressure or pressure relative to atmospheric ('gauge' pressure).

i think the extra 1m should take into consideration , am i right ? so , the working should be 30000 + (1.5x820x9.81) + (6 x1000x9.81) =13600(9.81)y ?

 

[rude man]

I think the extra 1m should take into consideration , am i right ?

Yes.

So, the working should be 30000 + (1.5x820x9.81) + (6 x1000x9.81) =13600(9.81)y ?

OK if the 30 kPa is gauge pressure.