What's wrong with this calculation simplified transformation circuit?

[pokie_panda]

Homework Statement

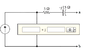
Use source transformation on the voltage source and series-connected impedance for the circuit shown here to find the equivalent current source and parallel-connected impedance. Continue the simplification by combining the two parallel current sources into an equivalent current source, and by combining the three parallel impedances into a single equivalent impedance.

Homework Equations

1/((1/Zr)+(1/Zl))
I=V/R

The Attempt at a Solution

First we simplify the voltage source into a current source
I=V/R
30<-90/15
=2<-90 A
to find the new current source we have I1+I2
=2<-90 A+4<90
=6<0A
Now to combine the resistor with the inductor
1/((1/Zr)+(1/Zl))
Therefore the new Z is
3+j9

 

[rude man]

Homework Statement

... to find the new current source we have I1+I2
=2<-90 A+4<90
=6<0A

That is not the correct addition. Express the two current sources as complex numbers and add per the rules of complex addition.

Now to combine the resistor with the inductor
1/((1/Zr)+(1/Zl))
Therefore the new Z is
3+j9

What happened to the 15 ohm resistor?

 

[pokie_panda]

Because we are simplifying we combine the resistor 15
Using 15 + (ZR*ZL)/(ZL+ZR)

 

[rude man]

Because we are simplifying we combine the resistor 15
Using


15 + (ZR*ZL)/(ZL+ZR)

" ... and by combining the three parallel impedances into a single equivalent impedance." That's what the problem said. So it gave you a hint right there.

The 15 ohm resistor is now in parallel with the 30 ohm and the inductor, so why are you adding its impedance to the parallel impedance of the other two components?

 

[pokie_panda]

so is this correct calculation

30V<-90 = I * 15 ohms
I = 2A<-90

The 15 ohm || 30 ohm = 10 ohms,

the 2A<-90 || 4A<90 = -j2 +j4 = j2 = 2<90

the 10 ohm || +j10 ohm = ((10) * (+j10)) / (10 +j10) = (+j100) / (10 +j10) = 5 +j5

 

[rude man]

30V<-90 = I * 15 ohms
I = 2A<-90

The 15 ohm || 30 ohm = 10 ohms,

the 2A<-90 || 4A<90 = -j2 +j4 = j2 = 2<90

the 10 ohm || +j10 ohm = ((10) * (+j10)) / (10 +j10) = (+j100) / (10 +j10) = 5 +j5

Ah, much better.