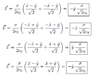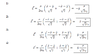emhelp100
- 14
- 0
Homework Statement
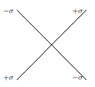
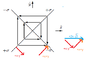
Two uniform infinite sheets of electric charge, one with charge density +o and the other with -o, intersect at right angles. Find and sketch the electric field \vec{E}
Homework Equations
\vec{E} = \frac{\sigma}{2e_0}
The Attempt at a Solution
Given solution:
[/B]
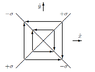
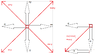
Numbered counterclockwise starting from \hat{x}
Can someone explain where the directions are coming from?
Why is it (\frac{\hat{x}-\hat{y}}{\sqrt{2}} + \frac{-\hat{x}-\hat{y}}{\sqrt{2}}) for 1. and etc?