paulimerci
- 287
- 47
- Homework Statement
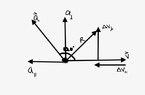
- During an interval of time, a tennis ball is moved so that the angle between the velocity and the acceleration of the ball is kept at a constant 120º. Which statement is true about the tennis ball during this interval of time?
(A) Its speed increases and it is changing its direction of travel.
(B) Its speed decreases and it is changing its direction of travel.
(C) Its speed remains constant, but it is changing its direction of travel.
(D) Its speed remains constant and it is not changing its direction of travel.
- Relevant Equations
- No equations!
I understand that when a tennis ball is in motion, the velocity vectors and acceleration vectors are pointing in the same direction. When the ball slows down, it is decelerating and comes to a stop. In the above statement, I understand that from the given angle, both vectors are pointing in the opposite direction and so ball is decelerating. My question here is how do I know it changes its direction?