Which statement is true? (Velocity and Acceleration of a Tennis Ball)

[Lnewqban]

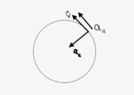
We do not need to concern ourselves with forces here. It is purely a kinematic question. Somehow the acceleration is made to have this relationship to the velocity. We do not care how.

I see that applicable to D) only.
If the tennis ball is changing trajectory, forces and accelerations are acting upon it.

As I see it, for the angle between the constantly changing direction of the velocity and the acceleration vectors of the ball to be kept at a constant angle, the constant direction of the weight force disqualifies to be coplanar with the non-linear trajectory.

 

[haruspex]

I see that applicable to D) only.

No, it applies throughout.

If the tennis ball is changing trajectory, forces and accelerations are acting upon it.

Sure, but it doesn’t matter what those forces are. All that matters is that as a result of them the ball moves as stated.

, the constant direction of the weight force

Which maybe countered perfectly by a constant upward force as one of the forces contributing to the motion.
If I hold a ball and move it along the sides of a vertical square, its motion is described completely by its location as a function of time. Given that, we can find the velocity and acceleration functions. We do not need the forces to determine them.

 

[erobz]

I think I have a way (not saying it the best way) to the solution...in theory.

let $y(x)$ be the path the particle is on

$\vec{a}$ has constant magnitude $a$, but is fixed at angle $\beta$ relative to $\vec{v}$.

The direction of $\vec{v}$ is given by the following relationship

$$ \frac{dy}{dx} = \tan \theta \tag{1}$$

Accelerations:

$$a_x = a \cos ( \theta + \beta) = \frac{dv_x}{dt} \tag{2} $$

$$ a_y = a \sin ( \theta + \beta ) = \frac{dv_y}{dt} \tag{3} $$

Using the Chain Rule and subbing (1):

$$ \frac{dy}{dx} \frac{dx}{dt} = \tan \theta v_x = v_y \tag{4}$$

Sub (4) into (3):

$$ \frac{d}{dt} ( \tan \theta v_x ) = a \sin ( \theta + \beta ) \tag{5}$$

Differentiate the LHS of (5):

$$ v_x \sec^2 \theta \frac{d \theta}{dt} + \frac{dv_x}{dt} \tan \theta = a \sin ( \theta + \beta ) \tag{6}$$

Sub (2) into (6) for $\frac{dv_x}{dt}$ and rearrange:

$$ \frac{d\theta}{dt} = \frac{a}{v_x \sec^2 \theta } (\sin ( \theta + \beta ) - \cos ( \theta + \beta) \tan \theta ) \tag{7}$$

Applying the Chain Rule to (7) to eliminate the parameter $t$:

$$ \frac{d \theta }{dx} = \frac{d\theta}{dt} v_x = \frac{a}{\sec^2 \theta } (\sin ( \theta + \beta ) - \cos ( \theta + \beta ) \tan \theta ) \tag{8}$$

In theory...solve (8) for $\theta (x)$, and solve (1) to find $y(x)$

I'm not brave enough to attempt an analytical approach. Perhaps it's just because trying cartesian coordinates it seems like an analytical pipe dream?

 

[erobz]

I almost gave up too quick... That whole RHS reduces dramatically by applying the sum difference formulas:

$$ \frac{d \theta }{dx} = a \sin \beta \cos \theta $$

I can get a little further:

$$ \ln \left| \frac{ \sec \theta + \tan \theta }{ \sec \theta_o + \tan \theta_o} \right| = a \sin \beta ( x - x_o ) $$

$$ \sec \theta + \tan \theta = \left( \sec \theta_o + \tan \theta_o \right) e^{ a \sin \beta ( x - x_o ) }$$

Then let $A$ = RHS and multiply through by $\cos \theta$:

$$ 1 + \sin \theta = A \cos \theta \implies 1 + \sqrt{1 - \cos^2 \theta} = A \cos \theta $$

That becomes:

$$ \cos \theta \left( \left( A^2 + 1 \right)\cos \theta - 2 A \right) = 0 $$

It should follow that ( ignoring solution $\theta = 90^{\circ}$:

$$ \cos \theta = \frac{2A}{A^2 + 1} $$

Then we can say that:

$$ \tan \theta = \frac{ \sqrt{ (A^2 + 1)^2 - 4A^2}}{2A }$$

Now, we are back to where I was before. Theoretically, you could then plug that into (1) and integrate to get $y(x)$.

$$ y(x) = \int dy = \int \frac{\sqrt{ (A^2 + 1)^2 - 4A^2} }{2A} dx $$

Where A is given by:

$$ A = \left( \sec \theta_o + \tan \theta_o \right) e^{ a \sin \beta ( x - x_o ) } $$

I thought it was kaput, until I noticed the difference of squares under the radical:

$$ \begin{aligned} y(x) &= \int \frac{\sqrt{ ( (A^2 + 1) - 2A )( (A^2 + 1) + 2A) } }{2A} dx \\ \quad \\ &= \int \frac{\sqrt{ (A-1)^2 ( A+1)^2 }}{2A} dx \\ \quad \\ &= \int \frac{A-1}{2A} dx +\int \frac{A+1}{2A} dx \end{aligned}$$

Surely this is a complete blunder...I'm getting that:

$$ \int \frac{A-1}{2A} dx +\int \frac{A+1}{2A} dx = \int dx = x-x_o $$

What...

$$ y(x) = x - x_o$$

??

 

[Lnewqban]

...
If I hold a ball and move it along the sides of a vertical square, its motion is described completely by its location as a function of time. Given that, we can find the velocity and acceleration functions. We do not need the forces to determine them.

Sorry @haruspex , I can’t understand your example.
Probably irrelevantly and wrongly, I have just tried to extend post #23 from @jbriggs444 by excluding the action of the unidirectional influence of g, as the problem in discussion gives the constrain of a rotating acceleration vector.

In my humble opinion, problems that may present vectors that change, rotate or move erratically without a natural reason are not helpful to students.
I hope that @paulimerci understands what the correct answer is and the natural or physical reason behind it.

 

[erobz]

Sorry @haruspex , I can’t understand your example.
Probably irrelevantly and wrongly, I have just tried to extend post #23 from @jbriggs444 by excluding the action of the unidirectional influence of g, as the problem in discussion gives the constrain of a rotating acceleration vector.

In my humble opinion, problems that may present vectors that change, rotate or move erratically without a natural reason are not helpful to students.
I hope that @paulimerci understands what the correct answer is and the natural or physical reason behind it.

This was just supposed to be a side exploration, @paulimerci is aware of that. However, I probably should have started a new thread.

Don't you think there is also an importance to understanding kinematics in physics? It's the mathematical framework in which we evaluate the physical laws. If you don't understand it well, you could end up doing what I did! What I don't understand is still a mystery to me, but it's clear I don't understand something. I could just as easily fumble "that something" applying the physical laws IMO.

Anyhow, just a thought experiment. I didn't mean to cause strife.

 

[kuruman]

I think this discussion is moving in a direction that is unlikely to help the OP. The original question is not about the trajectory of the tennis ball but about what happens to the speed and the direction of motion when the angle between the velocity and the acceleration is 120°. Whether that angle is instantaneously at that value or, as the problem states, it is maintained "during an interval of time" is irrelevant to which of the four listed choices is correct. If one of the answers is correct at an instant of time, it will be correct at subsequent instants of time as long as the angle is maintained at 120°.

Thus, let's project the ball at 45° relative to the horizontal and ask the question, "which of the four choices is correct when the velocity is at 30° relative to the horizontal?"

 

[erobz]

If anyone could just PM me where my first mistake is (unless it's all crap) I'd appreciate it.

 

[Lnewqban]

If anyone could just PM me where my first mistake is (unless it's all crap) I'd appreciate it.

What makes you believe that you made a mistake?
I see none.

 

[erobz]

What makes you believe that you made a mistake?
I see none.

It's telling me the trajectory is a line? The angle $\theta$ is fixed for a line trajectory ( and not just any line, a very specific $45^{\circ}$).

But the I'm also getting from the ODE:

$$ \frac{d \theta}{dx} = a \sin \beta \cos \theta $$

We get:

$$ \ln \left| \frac{ \sec \theta + \tan \theta }{ \sec \theta_o + \tan \theta_o} \right| = a \sin \beta ( x - x_o ) $$

Is that really yield a constant $\theta(x)$? Seems like a contradiction to me.

Even what @kuruman is saying in #37 could not be the case if that following math in #34 were correct?

 

[Lnewqban]

It's telling me the trajectory is a line? The angle $\theta$ is fixed for a line trajectory ( and not just any line, a very specific $45^{\circ}$).

But the I'm also getting from the ODE:

$$ \frac{d \theta}{dx} = a \sin \beta \cos \theta $$

We get:

$$ \ln \left| \frac{ \sec \theta + \tan \theta }{ \sec \theta_o + \tan \theta_o} \right| = a \sin \beta ( x - x_o ) $$

Is that really yield a constant $\theta(x)$? Seems like a contradiction to me.

Even what @kuruman is saying in #37 could not be the case if that following math in #34 were correct?

The problem shows the angle between the v and a vectors to be constant for a brief period of time, but allows freedom for the magnitudes of both vectors to change during the same time.
Therefore, to me, it seems to be physically possible.
I like @kuruman proposal.

 

[erobz]

The problem shows the angle between the v and a vectors to be constant for a brief period of time, but allows freedom for the magnitudes of both vectors to change during the same time.
Therefore, to me, it seems to be physically possible.
I like @kuruman proposal.

For the OP, they don't specify constant magnitude acceleration, just direction. So yeah, no problems there (that jump out at least).

My analysis is supposed to pertain to a trajectory where the magnitude of the acceleration is fixed, it is in that assumption that it seems like a contradiction to me, or something is not correct in what I've done. I honestly can't tell. By inspection I think it should be a spiral, and the math says its a line...that's a strong disconnect.

 

[Lnewqban]

I see, @erobz
The reason for the spiral is beyond my limited understanding.
Even @kuruman approach in post #37 would be an approximation for the beginning of the parabolic trajectory and for a very short period of time, as the angle between g and v will not stay constant.

 

[jbriggs444]

The reason for the spiral is beyond my limited understanding.

The spiral seems straightforward enough. I assume that we are taking the version of the problem where we have a projectile moving in a plane subject to an acceleration of constant magnitude always angled to the left and back at 120 degrees from the current velocity. An initial guess at the resulting trajectory would be a logarithmic spiral.

Clearly this leads to speed as a linear function of time. The projectile will cease moving at a future moment that can be easily calculated. At this time it will be at the center of the spiral. Velocity will cease to have a direction and the given description of the projectile's motion will cease to be predictive.

We might consider re-casting the problem to consider a projectile moving in the opposite manner -- spiralling outward from the center and using polar coordinates to track its motion.

 

[Lnewqban]

Thank you for that excellent explanation, @jbriggs444

 

[DrClaude]

I was intrigued so I did a numerical simulation. The initial conditions are $\vec{v} (0) = 10 \vec{i}$, $(x,y) = (0,0)$, and the acceleration is taken as $|\vec{a}| = 1$ (all units are arbitrary). The plot shows the $(x,y)$ position at time intervals of 1/10. The simulation ends at $t=20$ when $\vec{v} (0) =0$.

 

[erobz]

$$ \frac{d\theta}{dt} = \frac{a}{v_x \sec^2 \theta } (\sin ( \theta + \beta ) - \cos ( \theta + \beta) \tan \theta ) \tag{7}$$Applying the Chain Rule to (7) to eliminate the parameter $t$:

$$ \frac{d \theta }{dx} = \frac{d\theta}{dt} v_x = \frac{a}{\sec^2 \theta } (\sin ( \theta + \beta ) - \cos ( \theta + \beta ) \tan \theta ) \tag{8}$$

I figured out where I hung myself. It was a subtle mistake.

$$\frac{d\theta}{dt} = \frac{a}{v_x \sec^2 \theta } (\sin ( \theta + \beta ) - \cos ( \theta + \beta) \tan \theta ) \tag{7}$$

Applying the chain rule properly this time:

$$ \frac{d\theta}{dt} =\frac{d \theta}{dx} \frac{dx}{dt} = \frac{d \theta}{dx} v_x \tag{8}$$

Subbing (8) into (7), and reducing trigonometric terms:

$$ \frac{d \theta}{dx} = \frac{a}{v_x^2} \sin \beta \cos \theta \tag{9}$$

I'm sure no one cares, but I don't like to leave it like that.

 

[DrClaude]

I figured out where I hung myself. It was a subtle mistake.

$$\frac{d\theta}{dt} = \frac{a}{v_x \sec^2 \theta } (\sin ( \theta + \beta ) - \cos ( \theta + \beta) \tan \theta ) \tag{7}$$

Applying the chain rule properly this time:

$$ \frac{d\theta}{dt} =\frac{d \theta}{dx} \frac{dx}{dt} = \frac{d \theta}{dx} v_x \tag{8}$$

Subbing (8) into (7), and reducing trigonometric terms:

$$ \frac{d \theta}{dx} = \frac{a}{v_x^2} \sin \beta \cos \theta \tag{9}$$

I'm sure no one cares, but I don't like to leave it like that.

I tried my hand also at an analytical solution, but haven't succeeded yet. However, I am perplexed by your result. $d\theta/dt$ should be independent of $\theta$, by rotational symmetry.

 

[erobz]

I tried my hand also at an analytical solution, but haven't succeeded yet. However, I am perplexed by your result. $d\theta/dt$ should be independent of $\theta$, by rotational symmetry.

I don't know (I'm not smart enough to make that judgement call). Perhaps I bungled it even before I got to that step.

The units work out on that last ODE?

from (9) I need to work out $v_x$ as a function of $\theta$ or $x$. My hope would be to somehow go through:

$$ \frac{dv_x}{dt} = a \cos ( \theta + \beta ) $$

It's nice to have "spiral" confirmation with that simulation though! Thank you!

 

[erobz]

Oh, I think I see a path forward now... by the Chain Rule:

$$ \frac{dv_x}{dt} = v_x\frac{dv_x}{dx} = a \cos ( \theta + \beta) \tag{10} $$

By (9):

$$v_x^2 = a \sin \beta \frac{\cos \theta(x)}{ \theta'(x)} \tag{9'}$$

Differentiate (9') w.r.t $x$ (dropping the function notation):

$$ 2 v_x \frac{dv_x}{dx} =- a \sin \beta \left( \sin \theta + \frac{ \cos \theta}{ \theta'^2} \theta'' \right)$$

Then sub (10) into the result

$$ 2 \cos ( \theta + \beta ) = - \sin \beta \left( \sin \theta + \frac{ \cos \theta}{ \theta'^2} \theta'' \right) \tag{11}$$

Now, we can solve for $\theta(x)$...Theoretically and find $y(x)$ from (1).

However, given the form of (11), I think I'm not going to bother.

 

[paulimerci]

What happens during circular movement?
Could you have another acceleration vector that could be combined with the vector of centripetal acceleration in such a way that the resultant acceleration vector forms a constant angle with the velocity vector of the ball?

I understand that the velocity vector and acceleration vector are perpendicular to each other at every location on the circle in uniform circular motion at a constant speed because the acceleration vector points in the direction of the circle's center and the velocity is always tangent to the circle. Where should I draw "another acceleration vector" that you have pointed out in the above question?

 

[haruspex]

Where should I draw "another acceleration vector" that you have pointed out in the above question?

The centripetal acceleration is the acceleration component normal to the velocity, so any other acceleration must be parallel to it. That's the tangential component.

 

[haruspex]

Oh, I think I see a path forward now... by the Chain Rule:

$$ \frac{dv_x}{dt} = v_x\frac{dv_x}{dx} = a \cos ( \theta + \beta) \tag{10} $$

By (9):

$$v_x^2 = a \sin \beta \frac{\cos \theta(x)}{ \theta'(x)} \tag{9'}$$

Differentiate (9') w.r.t $x$ (dropping the function notation):

$$ 2 v_x \frac{dv_x}{dx} =- a \sin \beta \left( \sin \theta + \frac{ \cos \theta}{ \theta'^2} \theta'' \right)$$

Then sub (10) into the result

$$ 2 \cos ( \theta + \beta ) = - \sin \beta \left( \sin \theta + \frac{ \cos \theta}{ \theta'^2} \theta'' \right) \tag{11}$$

Now, we can solve for $\theta(x)$...Theoretically and find $y(x)$ from (1).

However, given the form of (11), I think I'm not going to bother.

It looks a bit nicer in $(s, \psi)$ coordinates. s is distance along the path, ψ is the angle the path makes to some fixed direction.
$\ddot s=a\cos(\theta)$
$\dot s\dot\psi=a\sin(\theta)$
That's not hard to solve; the hard part is figuring out what it looks like as a curve,

 

[paulimerci]

The centripetal acceleration is the acceleration component normal to the velocity, so any other acceleration must be parallel to it. That's the tangential component.

Does it look like this?

 

[haruspex]

Does it look like this?

Yes, though it does not have to be a circle. The diagram works for any section of the path short enough to be approximated as an arc of a circle.

 

[paulimerci]

Yes, though it does not have to be a circle. The diagram works for any section of the path short enough to be approximated as an arc of a circle.

Thank you, that makes sense!

 

[paulimerci]

Thank you, that makes sense!

Is there anything I missed or need to work on?

 

[Lnewqban]

I understand that the velocity vector and acceleration vector are perpendicular to each other at every location on the circle in uniform circular motion at a constant speed because the acceleration vector points in the direction of the circle's center and the velocity is always tangent to the circle. Where should I draw "another acceleration vector" that you have pointed out in the above question?

You understand correctly.
In accelerated circular movement there is a component of the acceleration that is tangential.

 

[paulimerci]

You understand correctly.
In accelerated circular movement there is a component of the acceleration that is tangential.

View attachment 321158

Oh, thank you so much. A lot is explained by these two diagrams. Worth it. I've learned something far more thoroughly than I anticipated.

 

[erobz]

It looks a bit nicer in $(s, \psi)$ coordinates. s is distance along the path, ψ is the angle the path makes to some fixed direction.

Indeed it does look quite tidy and succinct.

So $\psi$ is my $\theta$, and $\theta$ is my $\beta$. Is that correct?