gnarkil
- 26
- 0
Homework Statement
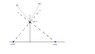
what is the electric field at point A (0,12) if there is charge c of 8*10^-9 coulombs at (16,0) and a charge d of 6*10^-9 coulombs at (-9,0)
determine x and y components of electric field (see diagram)
Homework Equations
electric field e = kq/r^2 where k is 9*10^9, q is charge, r is distance from point
The Attempt at a Solution
x components:
e_c = [(9*10^9)(8*10^-9)/(sqrt(16^2 + 12^2)^2 ]sin(phi)
= [(9*10^9)(8*10^-9)/(sqrt(16^2 + 12^2)^2 ] * [ 16 /(sqrt(16^2 + 12^2))]
= [(9*10^9)(8*10^-9)(16)] / [(16^2 + 12^2)^(3/2)]
= 0.144 Newtons/coulomb
e_d = [(9*10^9)(6*10^-9)/(sqrt(9^2 + 12^2)^2 ]sin(theta)
= [(9*10^9)(6*10^-9)/(sqrt(9^2 + 12^2)^2 ] * [ 9 /(sqrt(9^2 + 12^2))]
= [(9*10^9)(6*10^-9)(9)] / [(9^2 + 12^2)^(3/2)]
= 0.144 Newtons/coulomb
y components:
e_c = [(9*10^9)(8*10^-9)/(sqrt(16^2 + 12^2)^2 ]cos(phi)
= [(9*10^9)(8*10^-9)/(sqrt(16^2 + 12^2)^2 ] * [ 12 /(sqrt(16^2 + 12^2))]
= [(9*10^9)(8*10^-9)(12)] / [(16^2 + 12^2)^(3/2)]
= 0.108 Newtons/coulomb
e_d = [(9*10^9)(6*10^-9)/(sqrt(9^2 + 12^2)^2 ]cos(theta)
= [(9*10^9)(6*10^-9)/(sqrt(9^2 + 12^2)^2 ] * [ 12 /(sqrt(9^2 + 12^2))]
= [(9*10^9)(6*10^-9)(12)] / [(9^2 + 12^2)^(3/2)]
= 0.192 Newtons/coulomb
net electric force components:
x = 0.144+0.144 = 0.288 Newtons/coulomb
y = 0.108+0.192 = 0.300 Newtons/coulomb
my net components are wrong. why?