obad
- 12
- 0
Hi everyone,
I'm new here and I have a question to all the physicists out here in the forum.
I'm an aerospace engineering student and there is something that has been bothering me for
quite a while.
That is: Why does the static pressure of a fluid in motion change?
Don't get me wrong, I'm not a newbie in the area of fluid mechanics, aerodynamics and CFD.
I would say that I understand the principles of fluid flow and the laws governing fluid
motion pretty well. But what is really happening with the fluid when it accelerates and why
does the pressure, density and temperature change as a result?
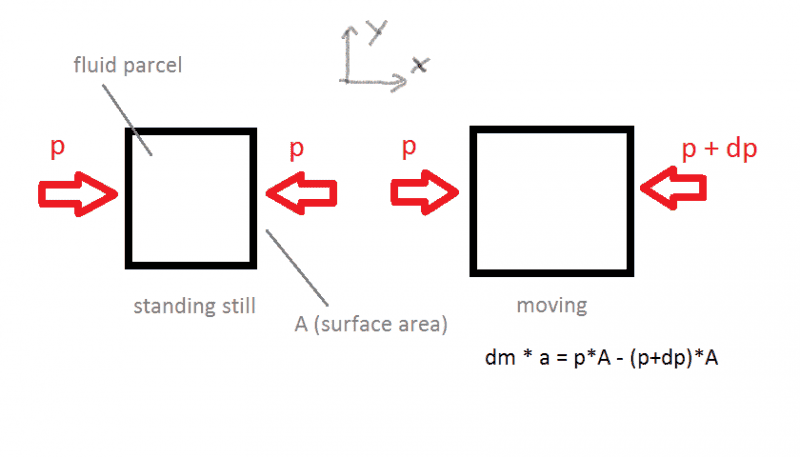
So I need a microscopic view of the physics that's going on in a moving fluid parcel. I
attached a sketch of two fluid parcels. One standing still and the other accelerating. By
applying the equation of motion to the moving parcel I was able to derive the Bernoulli
equation and well, of course the pressure changes when the fluid is accelerating. The
pressure is the engine of fluid flow.
But how exactly do the single molecules in this parcel behave during the acceleration and
how does their motion contribute to changes of the flow properties?
Is the parcel streched by different speeds on its boundaries?
If you already know the answer then go for it and make me life easier :)
Thanks!
If you want to read about my crazy theories then keep on reading.
Here are my theories about what's going on in the fluid:
First of all of course the static pressure is the pressure that can be measured at a wall
normal to the stream or if the fluid is enclosed in a container the static pressure can be
felt on every wall. The pressure is induced by the single molecules that hit the wall.
So now I thought, that when a fluid starts to move the random motion of the molecules is
straightened and the velocity component of the molecules normal to the wall is decreased,
which results in a weaker impulse and hence a decreased static pressure at the wall. But
still this model is not really satisfying ...
Maybe at the same time the observed fluid parcel streches and simultaniously its height
decreases, just as a strip of metal would do under tension. So in total the volume would
increase which contributes to less pressure and density. However in an incompressible fluid
the height would just decrease so much so that the volume stays constant and so does the
density. But what's happening with the pressure?
Well, my thoughts are pretty incomplete...I think if you have read this post till the end you can understand how desperatly I'm
searching for a solution.
I would really appreciate your help!
Cheers!
I'm new here and I have a question to all the physicists out here in the forum.
I'm an aerospace engineering student and there is something that has been bothering me for
quite a while.
That is: Why does the static pressure of a fluid in motion change?
Don't get me wrong, I'm not a newbie in the area of fluid mechanics, aerodynamics and CFD.
I would say that I understand the principles of fluid flow and the laws governing fluid
motion pretty well. But what is really happening with the fluid when it accelerates and why
does the pressure, density and temperature change as a result?
So I need a microscopic view of the physics that's going on in a moving fluid parcel. I
attached a sketch of two fluid parcels. One standing still and the other accelerating. By
applying the equation of motion to the moving parcel I was able to derive the Bernoulli
equation and well, of course the pressure changes when the fluid is accelerating. The
pressure is the engine of fluid flow.
But how exactly do the single molecules in this parcel behave during the acceleration and
how does their motion contribute to changes of the flow properties?
Is the parcel streched by different speeds on its boundaries?
If you already know the answer then go for it and make me life easier :)
Thanks!
If you want to read about my crazy theories then keep on reading.
Here are my theories about what's going on in the fluid:
First of all of course the static pressure is the pressure that can be measured at a wall
normal to the stream or if the fluid is enclosed in a container the static pressure can be
felt on every wall. The pressure is induced by the single molecules that hit the wall.
So now I thought, that when a fluid starts to move the random motion of the molecules is
straightened and the velocity component of the molecules normal to the wall is decreased,
which results in a weaker impulse and hence a decreased static pressure at the wall. But
still this model is not really satisfying ...
Maybe at the same time the observed fluid parcel streches and simultaniously its height
decreases, just as a strip of metal would do under tension. So in total the volume would
increase which contributes to less pressure and density. However in an incompressible fluid
the height would just decrease so much so that the volume stays constant and so does the
density. But what's happening with the pressure?
Well, my thoughts are pretty incomplete...I think if you have read this post till the end you can understand how desperatly I'm
searching for a solution.
I would really appreciate your help!
Cheers!