A circuit with non-linear devices

[JessicaHelena]

Homework Statement

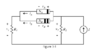
Two non-linear devices are placed in parallel in the circuit show in Figure 3-1. The resistors in the circuit have the following values: $R_1 = 2$ Ohms and $R_2 = 1$ Ohms.

The non-linear devices have different current-voltage (I-V) characteristics shown in Figure 3-2, where $I_S = 1A$ and $V_S = 1V$.

1. Given that the current source, I = 3A, calculate the numerical value for v1 and v2.

2. Now assume that the current source, I = 1A, and calculate the numerical value for v1 and v2.

Relevant Equations

KVL, KCL

I honestly don't know how to quite even begin this problem.

Looking at Fig 3-2, the slopes of the graphs are 1/R, and hence where the slopes are 0, we have infinite resistance, in which case current wouldn't flow through that resistor and hence simplify the circuit. So I was trying to find ways to use that, only I don't really know what the conditions are for $i_A, i_B, v_A, v_B$, and I don't think I could just randomly choose values I want to work with, could I?

 

[BvU]

we have infinite resistance

No we don't. It's just that V/I has a value that is not a constant.
Again, the use of the term R is misleading here.

 

[JessicaHelena]

@BvU

Okay—I take it then that maybe I shouldn't concern myself with R's, such as R_A and R_B?

From the graphs N_A and N_B, at I_S = 1 and V_S = 1, i_A = 1 and i_B = 0... That is however wrong since if I have i_B = 0, I would not have a valid V/I.

How else might I approach this?

 

[JessicaHelena]

going with the previous idea that i_A = 1 and i_B = 0, I get v_1 = iA*R_1 = 2V and i_2 = 3-1 = 2A and hence v_2 = i_2*R_2 = 2V. And they turn out to be right.

But using the same method, my answers to Q2—2V and 0V for v_1 and v_2—turn out to be wrong... so it does seem like my method itself is wrong.

 

[gneill]

So the trick is to find the operating point of the two mystery devices, then knowing the total current they are passing use that to work out the potential drops across the two resistors.

I would try to form a "collective" I-V curve for the pair. Since they are in parallel they must both share the same potential across them, and the currents that they pass will sum ($I = I_A + I_B$).

Now treat this new I-V curve as a single device. Draw load lines on this plot to find the operation point (I'd turn the current source and resistors into their Thevenin equivalent to simplify this step).

 

[Babadag]

vA=vB [Take different values up to I will be as required]

I=iA+iB+I2

I2=[(iA+iB)*R1+vA]/R2

iA=function(vA)

iB=function(vB)

function(vA)=

if vA<-1 iA=-1

if 0>vA>-1 iA=vA

if 0<vA<1 iA=vA

if vA>1 iA=1

function(vB)=

if vB<0 iA=1

if 0<vB<1 iB=1-vB

if vB>1 iB=vB-1