Sinusoidal
- 7
- 0
1. What is the acceleration of a skateboard down a ramp inclined at 19.5 degrees to the horizontal?
3.271 is the answer.
2. I know g Sin\vartheta is the equation to get it, but I don't get why it isn't g divided by Sin\vartheta
3. In my head I thought the picture was like this:
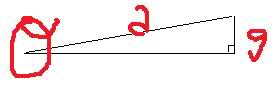
I know this should be something super easy, so please explain. haha
3.271 is the answer.
2. I know g Sin\vartheta is the equation to get it, but I don't get why it isn't g divided by Sin\vartheta
3. In my head I thought the picture was like this:
I know this should be something super easy, so please explain. haha