Puddles
- 12
- 0
Homework Statement
Given that a weight m1 is attached to a string going over a perfect pulley attached to another pulley suspending weight m2, and that weight m1 is on an incline with an angle of 37 degrees, find acceleration, tension, which mass hits the ground first, time needed to hit the ground, and max possible static friction. Note that m2 < m1. m1 is 2m from the bottom of the incline and m2 is 1m off the ground. Note that my teacher didn't actually write out a problem for us, so I'm trying to write this out as coherently as possible based on the drawing of a system we were given. So if something about this doesn't make sense please tell me.
Okay, so for a simple Atwood incline problem I kinda know what to do, but what about with double pulleys? It shouldn't be that confusing because I just have to use 2T for the weight accelerating upwards (m2) since it's attached to a pulley and not just the string attached to m1, right? I'll attach an image to see if that clears up what I mean. I've put down my work for most of the problem and I'm wondering if someone could help me check it or tell me how I can confirm I've done a problem like this right and self-check it. Also I completely don't know how to find the max possible static friction for a system to still work, can anyone explain this to me?
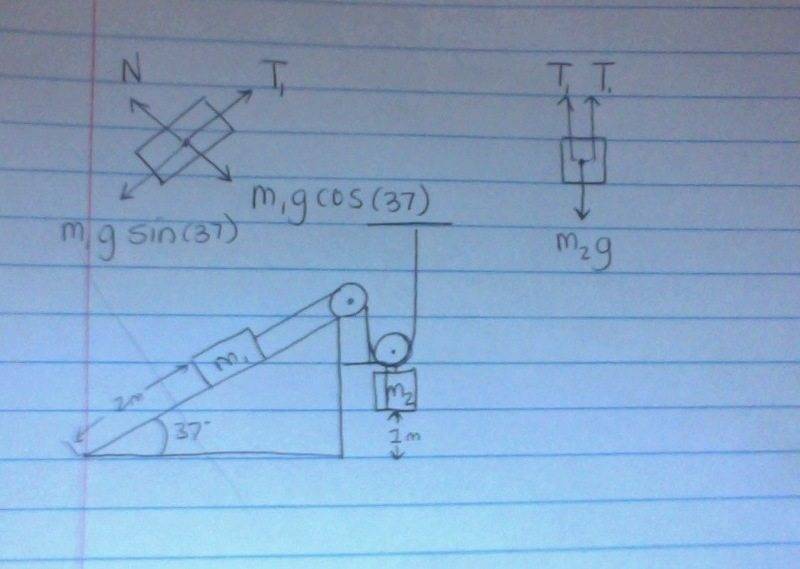
The attempt at a solution
T = m2*g/2
T = m2*g/2 = m1*g*sin 37°+m1*a
g cross
m2 = 1.2m1+2m1a
a1 = (m2-1.2m1)/2m1
2ℓ = 4.00 = a*t^2
t = √4/a = √8m1/(m2-1.2m1)
Vf1 = a1*t
a2 = 2h/t^2 =2(m2-1.2m1)/8m1 = (m2-1.2m1)/4m1 = a1/2
Where m1 = 10 kg and m2 = 15 kg,
a1 = (m2-1.2m1)/2m1 = (15-12)/20 = 3/20 = 0.15 m/sec^2
t = √8m1/(m2-1.2m1) = √8*10/(15-12) = 5.164 sec
Vf1 = a1*t = 0.15*5.164 = 0.775 m/sec
a2 = a1/2 = 0.15/2 = 0.075 m/sec^2
Vf2 = a2*t = Vf1/2 = 0.387 m/sec
Given that a weight m1 is attached to a string going over a perfect pulley attached to another pulley suspending weight m2, and that weight m1 is on an incline with an angle of 37 degrees, find acceleration, tension, which mass hits the ground first, time needed to hit the ground, and max possible static friction. Note that m2 < m1. m1 is 2m from the bottom of the incline and m2 is 1m off the ground. Note that my teacher didn't actually write out a problem for us, so I'm trying to write this out as coherently as possible based on the drawing of a system we were given. So if something about this doesn't make sense please tell me.
Okay, so for a simple Atwood incline problem I kinda know what to do, but what about with double pulleys? It shouldn't be that confusing because I just have to use 2T for the weight accelerating upwards (m2) since it's attached to a pulley and not just the string attached to m1, right? I'll attach an image to see if that clears up what I mean. I've put down my work for most of the problem and I'm wondering if someone could help me check it or tell me how I can confirm I've done a problem like this right and self-check it. Also I completely don't know how to find the max possible static friction for a system to still work, can anyone explain this to me?
The attempt at a solution
T = m2*g/2
T = m2*g/2 = m1*g*sin 37°+m1*a
g cross
m2 = 1.2m1+2m1a
a1 = (m2-1.2m1)/2m1
2ℓ = 4.00 = a*t^2
t = √4/a = √8m1/(m2-1.2m1)
Vf1 = a1*t
a2 = 2h/t^2 =2(m2-1.2m1)/8m1 = (m2-1.2m1)/4m1 = a1/2
Where m1 = 10 kg and m2 = 15 kg,
a1 = (m2-1.2m1)/2m1 = (15-12)/20 = 3/20 = 0.15 m/sec^2
t = √8m1/(m2-1.2m1) = √8*10/(15-12) = 5.164 sec
Vf1 = a1*t = 0.15*5.164 = 0.775 m/sec
a2 = a1/2 = 0.15/2 = 0.075 m/sec^2
Vf2 = a2*t = Vf1/2 = 0.387 m/sec