Dr-LucienSanchez
- 3
- 0
- Homework Statement
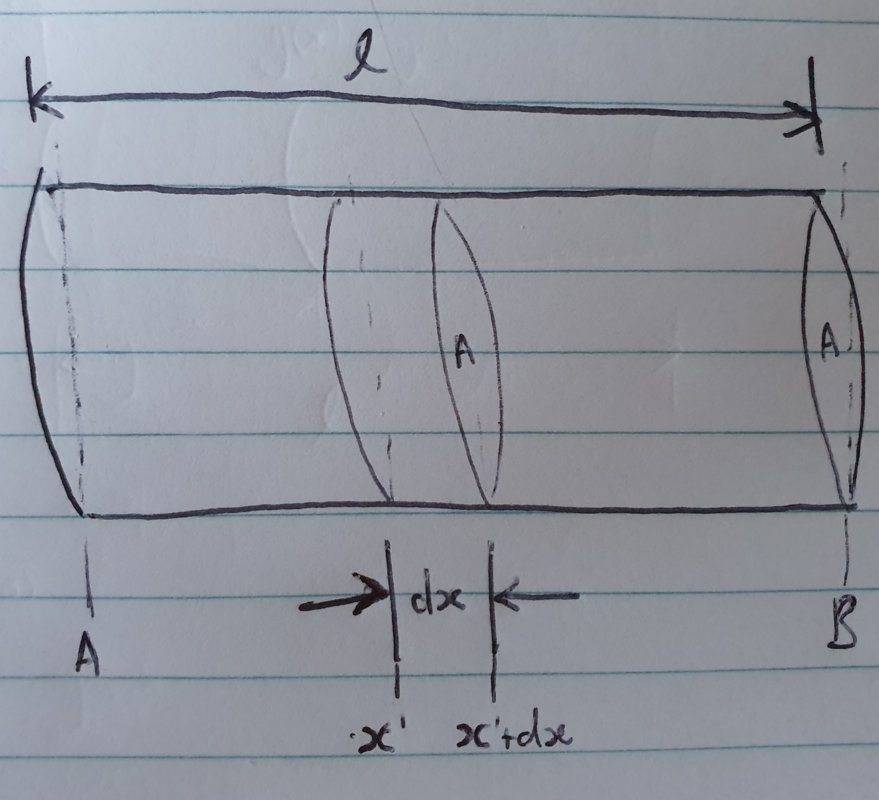
- The conductivity of a non-homogeneous rod (length l, cross sectional area A) varies linearly from the value ##g_a## at the end to the value ##g_b## at the end b; that is, at any point on the cross section of the rod lying at the distance x from a we have g (x) (below).
Divide the rod into discs of thickness dx, (i) compute the resistance of a typical disc, (ii) and show by integration that the total resistance of the rod is R (below)
- Relevant Equations
- Conductance at point x: (*) g(x) = g_a + (( g_b-g_a ) x ) / l
Total Resistance: (**) R = ( l/A ) * ( 1 / (g_b-g_a) ) * ln( g_b/g_a )
Between ends a and b of a conducting rod of length l and area A:
Average conductivity for non-homogeneous cylindrical conductors: (***) g_ave = (l / A)*G(ab)
Resistivity is the reciprocal of the conductivity i.e: (****) R(ab) = (l/gA), where g is the electric conductivity
(i) Dividing the rod into thicknesses of dx we get discs of area A with lengths=dx so using (****) we have the resistance of a typical disc (between point x' and x'+dx) as:
(1) ##R(x'dx)=\frac{dx}{g(x)A}##
(ii) Using (1) and (*) and the integrating from a to b of the entire rod we get:
##R(ab)=\int_{g_a}^{g_b}\frac{dx}{g_a+\frac{(g_b-g_a)x}{l}A}=\frac{l}{A}\int_{g_a}^{g_b}\frac{dx}{g_a l + (g_b-g_a)x}=\frac{l}{(g_b-g_a)A}ln(g_al+(g_b-g_a))##
Now my solution has a pesky ##g_al## which if it was not there then the total resistance would be the same as (**). However it is there which is why i need help.
I suspect that I have set up the problem incorrectly which leads me to integrate the wrong equation or I am missing something else.
Can anyone assist me to figure out where I have tripped up?
FYI this problem is from "Electromagnetic Fields and Waves" by Vladimir Rojansky page 11.
(1) ##R(x'dx)=\frac{dx}{g(x)A}##
(ii) Using (1) and (*) and the integrating from a to b of the entire rod we get:
##R(ab)=\int_{g_a}^{g_b}\frac{dx}{g_a+\frac{(g_b-g_a)x}{l}A}=\frac{l}{A}\int_{g_a}^{g_b}\frac{dx}{g_a l + (g_b-g_a)x}=\frac{l}{(g_b-g_a)A}ln(g_al+(g_b-g_a))##
Now my solution has a pesky ##g_al## which if it was not there then the total resistance would be the same as (**). However it is there which is why i need help.
I suspect that I have set up the problem incorrectly which leads me to integrate the wrong equation or I am missing something else.
Can anyone assist me to figure out where I have tripped up?
FYI this problem is from "Electromagnetic Fields and Waves" by Vladimir Rojansky page 11.
Last edited by a moderator: