sareba
- 8
- 0
Homework Statement
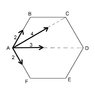
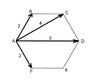
In a regular hexagon, ABCDEF, forces of magnitude 2N, 4N, 3N and 2N act along the lines AB, AC, AD and AF respectively. Find the equilbrant of the given forces and verify that is equal and opposite to their resultant.
The Attempt at a Solution
I realized that AB + BC is equal to AC, which is 4N, so BC should be 2N and AC + CD is equal to AD, which is equal to 3N, so CD should be equal to -1N? but also since AC is parallel to and twice as much as BC it should be 4N but it is 3N so which of my assumption is wrong? Also resolving didnt get me the right answer maybe i didnt do it right.
The answer is 8.7 N at 46.7° to BA.
P.S I am new to this forum so go easy if i didnt post it right or anything. :D