Cloruro de potasio
- 30
- 1
- Homework Statement
- Given the circuit of Fig. 13-6, with L = 4mH, C=2$\muF$, R1 = 25 ohms, R2 = 40 Ohms. Find the following set of frequencies.
a) where $\omega = 1/\sqrt{LC}$
b) where the impedance is maximum.
c) where the current through R1 is in phase with the generatori voltage.
- Relevant Equations
- Z = R + i(\omegaL - 1/\omegaC)
Series asociation of Z: $Z_eq = Z_1 + Z_2 + ...$
Association of Z in parallel: $Z_eq^-1 = Z_1^-1 + Z_2^-1 + ...$
Hello,
I have been thinking about this problem for a few hours, and I do not understand how I should proceed to solve it correctly. Section a is very simple, just substitute in the expression that gives us the values of L and C that the statement gives us.
However, when I get to section b, I have encountered the problem that what I have done is calculate the modulus of the equivalent impedance, and from there, try to derive with respect to $ \ omega $, in order to try to find the frequency value for which the impedance is maximum.
However, the expression of Z that remains is very long and complicated, both to calculate its module, and to derive, so I interpret that there must be another way to solve the exercise more easily, which has not occurred to me.
I leave you the figure on which the exercise deals, and the value of impedance that is obtained
Thank you very much in advance and regards
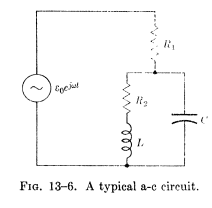
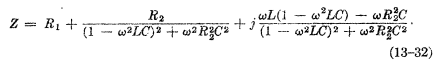
I have been thinking about this problem for a few hours, and I do not understand how I should proceed to solve it correctly. Section a is very simple, just substitute in the expression that gives us the values of L and C that the statement gives us.
However, when I get to section b, I have encountered the problem that what I have done is calculate the modulus of the equivalent impedance, and from there, try to derive with respect to $ \ omega $, in order to try to find the frequency value for which the impedance is maximum.
However, the expression of Z that remains is very long and complicated, both to calculate its module, and to derive, so I interpret that there must be another way to solve the exercise more easily, which has not occurred to me.
I leave you the figure on which the exercise deals, and the value of impedance that is obtained
Thank you very much in advance and regards