engineer_dave
- 35
- 0
Circuit Nodal voltage question...please help out thanks!
The question is as follows:
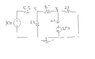
Start with KCL for the nodes and write the node voltage equations for the nodes V1 and v2 in the circuit (diagram is attached to this post). They do not want me to solve the equations but just simplify to gather the coefficents.
KCL
I marked node one where v1 is. So for node 1 it would be (v1- 30)/10 + (v1-v2)/8 + v1/6=0
I marked node 2 where v2 is. So for node 2 it would be (v2- v1)/8 + (v2+20)/4=0
Still, I am not that sure about my node 2 equations although my node 1 may be correct. Please help! THanks!
Homework Statement
The question is as follows:
Start with KCL for the nodes and write the node voltage equations for the nodes V1 and v2 in the circuit (diagram is attached to this post). They do not want me to solve the equations but just simplify to gather the coefficents.
Homework Equations
KCL
The Attempt at a Solution
I marked node one where v1 is. So for node 1 it would be (v1- 30)/10 + (v1-v2)/8 + v1/6=0
I marked node 2 where v2 is. So for node 2 it would be (v2- v1)/8 + (v2+20)/4=0
Still, I am not that sure about my node 2 equations although my node 1 may be correct. Please help! THanks!