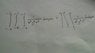You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Coulomb's law and Electric field intensity problem
- Thread starter rizwanibn
- Start date
AI Thread Summary
The discussion revolves around solving a problem related to Coulomb's law and electric field intensity, where the original poster struggles to match their answer with the textbook solution. They emphasize the importance of correctly interpreting the absolute value in the inequality, which defines the range of x. A suggestion is made to consider the integration volume as eight small cubes, each measuring 0.1, positioned at the corners of a larger cube measuring 0.4. The conversation highlights that the symmetry of the cubes leads to cancellation of opposite signs in calculations. Ultimately, the participants express a clearer understanding of the problem and its solution.
Engineering news on Phys.org
blue_leaf77
Science Advisor
- 2,637
- 786
Be carefull with the absolute sign in the inequality. ##0.1 \leq |x| \leq 0.2 = (x\leq -0.1 \cup x\geq 0.1) \cap -0.2\leq x \leq 0.2##.
blue_leaf77
Science Advisor
- 2,637
- 786
Yes, I think that should give you the correct answer.
rizwanibn
- 5
- 0
Is it addition of subtraction in between...?
blue_leaf77
Science Advisor
- 2,637
- 786
On a second thought, I think your the integration volume should be eight small cubes of sides 0.1 at each corner of a large cube of sides 0.4. As illustration for x-y plane, see picture below. The intersection area in that picture actually forms four long bar of square cross section when put in a 3D coordinate. If you add the last region corresponding to the inequality for ##z##, you should get 8 cubes as the integration volume.
Attachments
Last edited:
rizwanibn
- 5
- 0
Thanks very much.
Got a very good understanding of it.
So all the cubes has a pair of opposite sign and they cancel out each other.
Got a very good understanding of it.
So all the cubes has a pair of opposite sign and they cancel out each other.
blue_leaf77
Science Advisor
- 2,637
- 786
You have to do the calculation to see if that's true.
Similar threads
- Replies
- 6
- Views
- 1K
- Replies
- 20
- Views
- 3K
- Replies
- 2
- Views
- 1K
- Replies
- 17
- Views
- 2K
- Replies
- 6
- Views
- 1K
- Replies
- 8
- Views
- 1K
- Replies
- 5
- Views
- 2K
- Replies
- 24
- Views
- 2K
- Replies
- 1
- Views
- 1K
- Replies
- 2
- Views
- 771
Hot Threads
-
Spain’s power outage
- Started by Guineafowl
- Replies: 59
- Electrical Engineering
-
PVC Induction Heating Coil Design (early thoughts)
- Started by RickDelta
- Replies: 51
- Electrical Engineering
-
Using Latex Code for Circuit Diagrams
- Started by neilparker62
- Replies: 25
- Electrical Engineering
-
What is the difference between a switch leg and a hot leg?
- Started by sevensages
- Replies: 37
- Electrical Engineering
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 91
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math