- #1
JohnnyGui
- 796
- 51
Hello,
I have a question regarding the following picture:
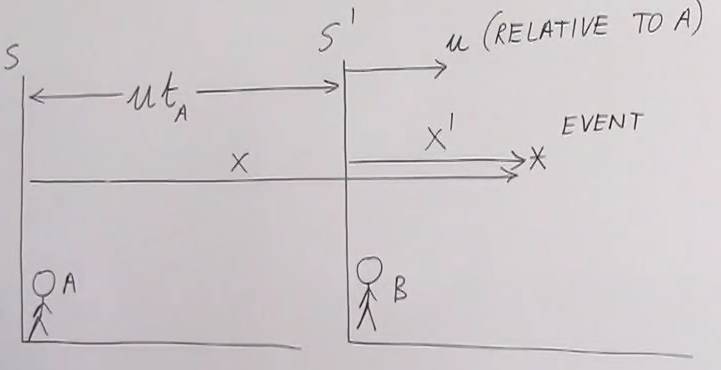
Here, person B is moving in his S’ reference frame with a speed of u relative to Person A, who is in his reference frame S. An event shown by a star (*) happens after tA time according to A.
The distance of that event is a distance of x according to Person A. The distance of that event is a distance of x’ according to Person B. From this we can relate x’ and x by using the Lorentz length contraction formula.
Person A will calculate that his own distance x is equal to:
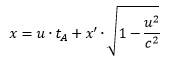
Here’s my question; what is the relationship between x’ and x according to Person B in a formula in which person B uses his own time tB? So I’d want to relate x, x’ and tB in a formula. How do you do that by concluding it from the picture instead of rewriting my given formula for Person A?
I have a question regarding the following picture:
Here, person B is moving in his S’ reference frame with a speed of u relative to Person A, who is in his reference frame S. An event shown by a star (*) happens after tA time according to A.
The distance of that event is a distance of x according to Person A. The distance of that event is a distance of x’ according to Person B. From this we can relate x’ and x by using the Lorentz length contraction formula.
Person A will calculate that his own distance x is equal to:
Here’s my question; what is the relationship between x’ and x according to Person B in a formula in which person B uses his own time tB? So I’d want to relate x, x’ and tB in a formula. How do you do that by concluding it from the picture instead of rewriting my given formula for Person A?