RealityMechanics
- 1
- 0
- Homework Statement
- How would the mass flow rate equation in this scenario change if the flow is reversed?
- Relevant Equations
- See the image. A variation of Bernoulli's Equation.
Alright, this is more of a conceptual question than a HW question that will nonetheless help me design something. In the attached image, air is flowing through a large area tube and then a small area tube from right to left. A collaborator previously figured out the equation for measuring the flow rate in this way, which I placed beneath this diagram I made. I know this equation is correct because I tested out the measurements experimentally. In this image, the cylinders just represent the location of pressure sensors constantly logging the pressure at that location.

I would like to write another equation, however that represents the flow rate if instead, the air was sucked out from the right side. So essentially the air travels in reverse all the way from the open hole on the left to the right side of the tube. I attached an image I made representing this.
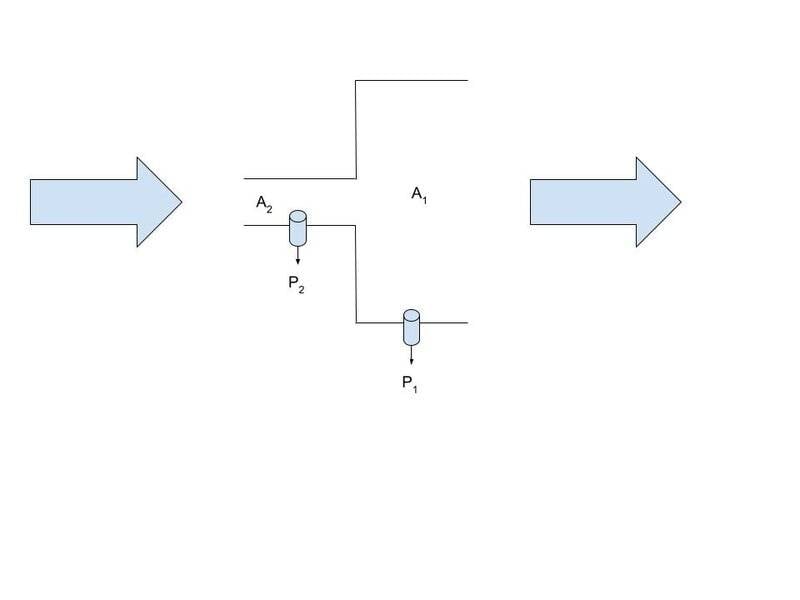
Here are a couple things I would like to point out that has been confusing me in figuring this out.
1. Pdiff is always going to be P1-P2 at any given instant. We do not know what P1 and P2 individually is. That's just the way the pressure sensor works.
2. The first equation was created from the perspective of the right hand side blowing air into the tube. I want this equation to still be from the same right side perspective, or something sucking the air out of the tube.
3. In the original scenario, Pdiff is always positive since P1 > P2. However, in this scenario I am trying to figure out, Pdiff is always going to be negative since P2 > P1. You cannot square root a negative. Perhaps, an absolute value is needed for Pdiff? Can we get these flow rates to be negative since the perspective is the same (right side) but now the air is being sucked out instead of blown in?
By the way, all horizontal measurements are symmetrical, if that matters. The length of both area tubes are the same, and the pressure sensors are equidistant from the ends of both area tubes and the center.
Any help will be much appreciated.
I would like to write another equation, however that represents the flow rate if instead, the air was sucked out from the right side. So essentially the air travels in reverse all the way from the open hole on the left to the right side of the tube. I attached an image I made representing this.
Here are a couple things I would like to point out that has been confusing me in figuring this out.
1. Pdiff is always going to be P1-P2 at any given instant. We do not know what P1 and P2 individually is. That's just the way the pressure sensor works.
2. The first equation was created from the perspective of the right hand side blowing air into the tube. I want this equation to still be from the same right side perspective, or something sucking the air out of the tube.
3. In the original scenario, Pdiff is always positive since P1 > P2. However, in this scenario I am trying to figure out, Pdiff is always going to be negative since P2 > P1. You cannot square root a negative. Perhaps, an absolute value is needed for Pdiff? Can we get these flow rates to be negative since the perspective is the same (right side) but now the air is being sucked out instead of blown in?
By the way, all horizontal measurements are symmetrical, if that matters. The length of both area tubes are the same, and the pressure sensors are equidistant from the ends of both area tubes and the center.
Any help will be much appreciated.