thisischris
- 26
- 1
Hello!
I'm having a bit of a struggle understanding the logic behind these two questions.
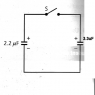
A 2.2 uF capacitor is charged to a potential of 15V, and a 3.3uF capacitor is charged to a potential of 30V.
The capacitors are then joined together as in the circuit diagram. When the switch s is closed, the charge re-distributes between the capacitors. Explain why the final voltage across each capacitor is the same.
Answer: Capacitors are in parallel.
I sort of agree that the voltage would be the same otherwise charge would 'flow' from one point to another. I don't understand how them being in parallel explains this however.
Suggest why the calculated value of energy stored by the capacitors (1.6 x10-3J) is less than the total energy that would be stored by the capacitors individually.
Answer: Work is done redistributing charge.
Is this due to resistance/internal resistance(?). However we haven't accounted for it (I think?) so I don't see why it should be lower, unless the question refers to a actual experiment that may take place?
Thank you
I'm having a bit of a struggle understanding the logic behind these two questions.
A 2.2 uF capacitor is charged to a potential of 15V, and a 3.3uF capacitor is charged to a potential of 30V.
The capacitors are then joined together as in the circuit diagram. When the switch s is closed, the charge re-distributes between the capacitors. Explain why the final voltage across each capacitor is the same.
Answer: Capacitors are in parallel.
I sort of agree that the voltage would be the same otherwise charge would 'flow' from one point to another. I don't understand how them being in parallel explains this however.
Suggest why the calculated value of energy stored by the capacitors (1.6 x10-3J) is less than the total energy that would be stored by the capacitors individually.
Answer: Work is done redistributing charge.
Is this due to resistance/internal resistance(?). However we haven't accounted for it (I think?) so I don't see why it should be lower, unless the question refers to a actual experiment that may take place?
Thank you
Attachments
Last edited: