Electric charges and fields: Semicircular charge distributions

AI Thread Summary
The discussion revolves around calculating the electric field intensity at point O due to a semicircular charge distribution with a linear charge density of 1 microcoulomb per meter. Participants express uncertainty about how to progress after determining that the electric fields from two straight lines would cancel each other out. There is a call for clarification on the formulas or logic needed to find the electric fields from the semicircles. The need for relevant equations and a structured approach to solving the problem is emphasized. Overall, the conversation highlights the challenges of applying theoretical concepts to practical problems in electrostatics.
Ujjwal28
Messages
32
Reaction score
0

Homework Statement


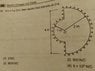
If linear charge density is equal to 1micro coulomb per meter, then what is the electric field intensity at O?

Homework Equations

The Attempt at a Solution


The electric fields due to the two straight lines should cancel out.. But how to progress further? Please let me know...
 

Attachments

  • IMG_20160423_181641.jpg
    IMG_20160423_181641.jpg
    47.1 KB · Views: 380
Physics news on Phys.org
Ujjwal28 said:
But how to progress further?
Finding the fields due to the semi-circles, is it not?
 
Ok so... How is it done? Is there any formula or logic behind that?
 
Ujjwal28 said:
Ok so... How is it done? Is there any formula or logic behind that?
That should be your part to find the related formula in the "Relevant equations" section of the template.
 
Ok can you please elaborate on how to find it? And how to proceed with the problem?
 

Thread 'Struggling to understand the concept of this question (ice cube in water optics question)'

TL;DR Summary: I came across this question from a Sri Lankan A-level textbook. Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water. I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
View full post »
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Can a dipole be modeled as a point charge?
Replies
10
Views
522
Electric field external to Conducting Hollow Sphere with charge inside
Replies
23
Views
3K
Charge on inner/outer surfaces of two large parallel conducting plates
Replies
11
Views
3K
Electric field due to n charges
Replies
6
Views
2K
Discontinuity in an Electric line of force
Replies
12
Views
2K
Electric field at a point close to the centre of a conducting plate
Replies
7
Views
2K
Find the electric field of a long line charge at a radial distance
Replies
1
Views
2K
Electric field at a point within a charged circular ring
2
Replies
68
Views
7K
Why Does the Electric Field Sum Instead of Cancel with Opposite Charges?
Replies
6
Views
2K
Why are the electrostatic field lines normal to a charged conductor?
Replies
10
Views
1K

Hot Threads

Recent Insights

Back
Top