Electric field distribution inside a truncated cone

[vinven7]

Homework Statement

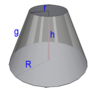
Consider a truncated cone as shown in the figure. the material of the cone is a dielectric with top and bottom electrodes of different radii. Now a potential difference is applied across the capacitor - by connecting it to a battery - let's say. This creates an electric field distribution within the material inside the cone. How can we model the electric field distribution? If 'z' is the height from the bottom and r is the radial distance from the axis of the cone (parallel to the electrodes), what is the function E(z,r) at any point (z,r) within the cone?
Any ideas, suggestions, references, partial or full solutions will be greatly appreciated. Thanks

The Attempt at a Solution

To begin with, I am not sure if this sets up a uniform or a non - uniform electric field. I have read that the electric field lines have to be perpendicular to the electrodes as they are equipotential, and also that they have to parallel to the edges. By background is not in electrical sciences, so I am not even able to say if this is a simple or complicated problem.

 

[mfb]

It is simple if you make some approximations, like (R-r) << h. It is hard and requires a two-dimensional simulation without that (or similar) assumption(s).