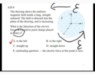
SUMMARY
The discussion focuses on the electric force experienced by a charge in a solenoid, specifically addressing the implications of changing magnetic flux as described by Faraday's law of electromagnetic induction. Participants clarify that the direction of the induced electric field, represented as ## \vec{E}_{induced} ##, is crucial for determining the force on a positive charge, which is calculated using the equation ## \vec{F}=q(\vec{E}+\vec{v} \times \vec{B}) ##. The right-hand rule is employed to establish the relationship between current, magnetic field, and force direction. The importance of the term "increasing with time" in the problem statement is emphasized, highlighting its role in generating an electromotive force (EMF).
PREREQUISITES
- Understanding of Faraday's law of electromagnetic induction
- Familiarity with the right-hand rule for magnetic forces
- Knowledge of electric field and force equations in electromagnetism
- Basic concepts of magnetic flux and its changes over time
NEXT STEPS
- Study the applications of Faraday's law in real-world electromagnetic systems
- Learn about the implications of induced electric fields in circuits
- Explore the relationship between magnetic fields and electric currents in solenoids
- Investigate the effects of varying magnetic fields on charged particles
USEFUL FOR
Students of physics, educators teaching electromagnetism, and engineers working with electromagnetic systems will benefit from this discussion.