Kaushik
- 282
- 17
- Homework Statement
- A container of height 3m and width 5m is filled with water upto 2 m. It is accelerated such that the water is at the brim (it is about to spill). When it moves with this acceleration find the force acting per unit width on the vertical wall.
- Relevant Equations
- I got ##a = 4 \frac{m}{s^2}##
A container of height 3m and width 5m is filled with water upto 2 m. It is accelerated such that the water is at the brim (it is about to spill). When it moves with this acceleration find the force acting per unit width on the vertical wall.
I found the acceleration for the condition provided but how to find the force per unit width?
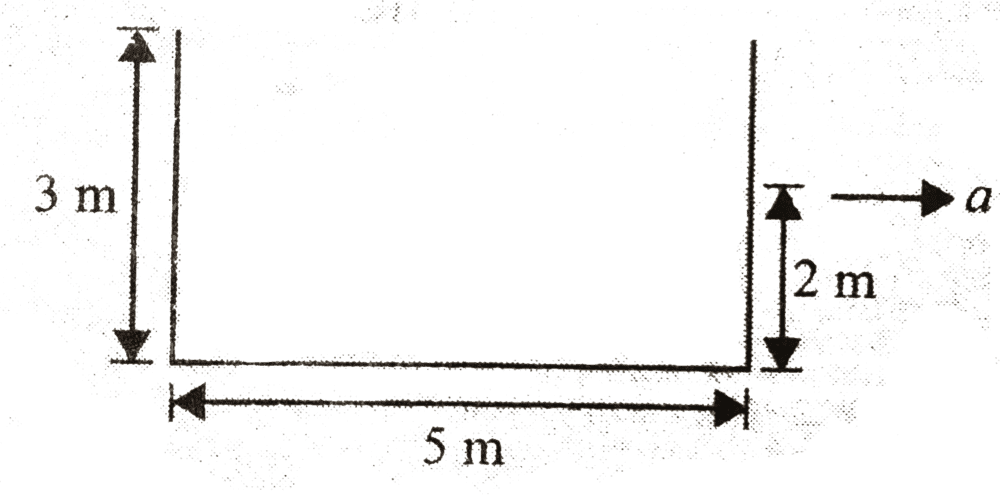
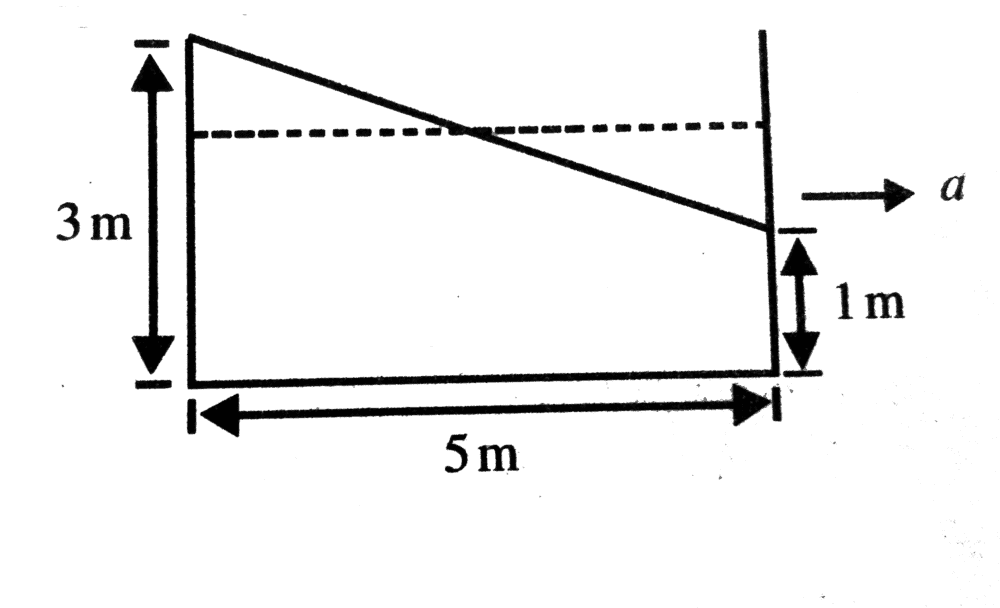
I found the acceleration for the condition provided but how to find the force per unit width?
Last edited: