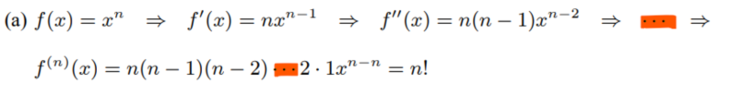member 731016
- Homework Statement
- Please see below
- Relevant Equations
- Please see below
For part(a),
The solution is,
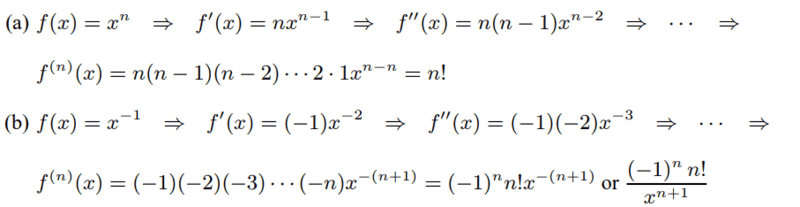
However, I am having trouble understanding their finial formula. Does anybody please know what the floating ellipses mean? I have only seen ellipses that near the bottom like this ##...## I am also confused where they got the ##2 \cdot 1## from.
When solving this problem, in addition to finding the 1st and 2nd derivatives, I also found the 3rd and 4th derivatives, but I guess I didn't need the last two to find the pattern?
Many thanks!
The solution is,
However, I am having trouble understanding their finial formula. Does anybody please know what the floating ellipses mean? I have only seen ellipses that near the bottom like this ##...## I am also confused where they got the ##2 \cdot 1## from.
When solving this problem, in addition to finding the 1st and 2nd derivatives, I also found the 3rd and 4th derivatives, but I guess I didn't need the last two to find the pattern?
Many thanks!
Attachments
Last edited by a moderator: