- #1
Ocasta
- 40
- 0
I want to apologize ahead of time for my apparent inability to get LaTeX to display properly.
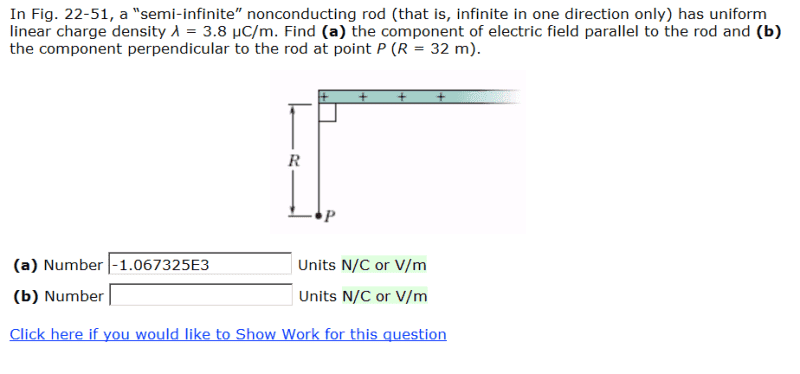
λ = 3.8 x 10^(-6) C/m
R = 32m
r = magnitude of the hypotenuse (the book's convention, a poor choice IMHO)
r = [itex] \sqrt{R^2 + x^2} [/itex]
k = 8.988 x 10^9
P:(0,-32)
cosθ = x/r
a→∞
[itex] dE = λk \int_0^a \frac{dx}{r^2}[/itex]
We're supposed to figure out the overall field strength, which is finite.
[itex]dE = λk \int_0^a \frac{dx}{r^2} [/itex]
[itex]dE_x = λk \int_0^a \frac{dx}{r^2} cosθ [/itex]
[itex]dE_x = λk \int_0^a \frac{dx}{r^2} \frac{x}{r}[/itex]
[itex]
dE_x = λk \int_0^a \frac{xdx}{r^3}
[/itex]
[itex]
u = R^2 + x^2 → \frac{du}{2} = xdx
[/itex]
[itex]
dE_x = λk \int_0^a (u)^{-3/2} du
[/itex]
[itex]
dE_x = λk [ -2 u^{-1/2} ]_0^a
[/itex]
[itex]
dE_x = -2λk [ (R^2 + x^2)^{-1/2} ]_0^a
[/itex]
[itex]
dE_x = -2λk [ \frac{1}{\sqrt{R^2 + x^2}} ]_0^a
[/itex]
[itex]
dE_x = -2λk [ \frac{1}{\sqrt{R^2 + \inf^2}} - \frac{1}{\sqrt{R^2}} ]
[/itex]
[itex]
dE_x = -2λk [ 0 - \frac{1}{\sqrt{R^2}} ]
[/itex]
[itex]
dE_x = -2λk [ \frac{1}{R} ]
[/itex][itex]
dE_x ≈ -2.13465 x 10^3
[/itex]
Homework Statement
λ = 3.8 x 10^(-6) C/m
R = 32m
r = magnitude of the hypotenuse (the book's convention, a poor choice IMHO)
r = [itex] \sqrt{R^2 + x^2} [/itex]
k = 8.988 x 10^9
P:(0,-32)
cosθ = x/r
a→∞
Homework Equations
[itex] dE = λk \int_0^a \frac{dx}{r^2}[/itex]
The Attempt at a Solution
We're supposed to figure out the overall field strength, which is finite.
[itex]dE = λk \int_0^a \frac{dx}{r^2} [/itex]
[itex]dE_x = λk \int_0^a \frac{dx}{r^2} cosθ [/itex]
[itex]dE_x = λk \int_0^a \frac{dx}{r^2} \frac{x}{r}[/itex]
[itex]
dE_x = λk \int_0^a \frac{xdx}{r^3}
[/itex]
[itex]
u = R^2 + x^2 → \frac{du}{2} = xdx
[/itex]
[itex]
dE_x = λk \int_0^a (u)^{-3/2} du
[/itex]
[itex]
dE_x = λk [ -2 u^{-1/2} ]_0^a
[/itex]
[itex]
dE_x = -2λk [ (R^2 + x^2)^{-1/2} ]_0^a
[/itex]
[itex]
dE_x = -2λk [ \frac{1}{\sqrt{R^2 + x^2}} ]_0^a
[/itex]
[itex]
dE_x = -2λk [ \frac{1}{\sqrt{R^2 + \inf^2}} - \frac{1}{\sqrt{R^2}} ]
[/itex]
[itex]
dE_x = -2λk [ 0 - \frac{1}{\sqrt{R^2}} ]
[/itex]
[itex]
dE_x = -2λk [ \frac{1}{R} ]
[/itex][itex]
dE_x ≈ -2.13465 x 10^3
[/itex]
Last edited: