ravensfan
- 2
- 0
Homework Statement
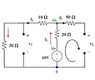
Find the voltage across the capacitors in the circuit given under DC conditions.
Homework Equations
V=IR
The Attempt at a Solution
The solution is already given (the picture attached was obtained from the solution manual. I have a difficult time understanding how they arrived to that answer. V1 and V2 are really capacitors, but since this is in DC conditions, they are treated as open circuits.
I think I understand why V1 is 30v - since this circuit is essentially 3 resistors in series on the left side, all I'd need to do is find the current, then use that current across the 30 ohm resistor to find voltage, and since that resistor is in parallel with the capacitor, the voltage would be the same.
The right side is what I do not understand. Why would the voltage V2 be equal to 60-20*I1?
Thanks.