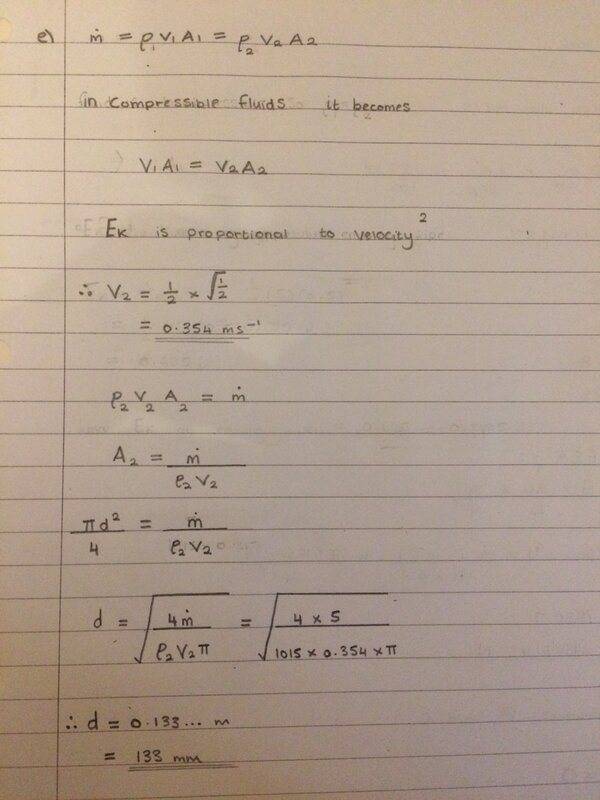The discussion revolves around a problem involving fluid velocity and pipe diameter using the continuity equation. Participants express concerns about inconsistencies in the problem statement, particularly regarding the mass flow rate calculation, which should be approximately 0.64 kg/s instead of the stated 5 kg/s. There is confusion about whether the fluid's velocity of 0.5 m/s applies before entering the 40 mm pipe and the lack of pressure information complicates the use of Bernoulli's equation. The problem is deemed poorly worded, leading to misinterpretations of key concepts like pressure and density. Overall, the consensus is that the problem's formulation needs clarification for accurate analysis.