Hamiltonian
- 296
- 193
- Homework Statement
- A system consists of a thin charged wire ring of radius ##R## and a very long uniformly charged rod oriented along the axis of the ring, with one of its coinciding with the centre of the ring. the total charge of the ring is equal to ##q##. The charge of the rod(per unit length) is equal to ##\lambda##. Find the interaction force between the ring and the rod
- Relevant Equations
- ##\vec F = q\vec E##
This is the initial setup of the problem:
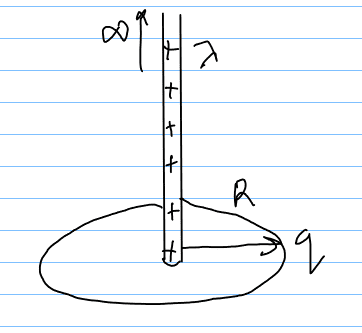
The electric field due to the ring is:
$$E = \int\frac{k(dq)}{(\sqrt{R^2 + x^2})^2}\frac{x}{\sqrt{R^2 + x^2}} = \frac{kqx}{(R^2 + x^2)^{3/2}}$$
the force on the rod due to this Electric field produced by the ring is:
Consider a differential element ##dq## of the rod on which the force is:
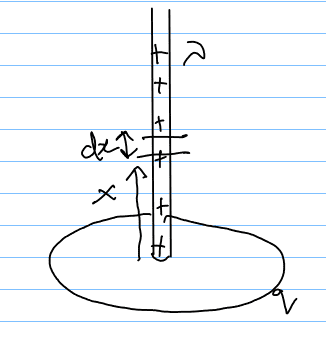
$$dF = E(dq) = E\lambda(dx)\frac{kqx\lambda(dx)}{(x^2 + R^2)^{3/2}}$$
The total force on the rod by the ring will be:
$$F = kq\lambda\int_{0}^{\infty}\frac{x}{(x^2 + R^2)^{3/2}} dx = -kq\lambda\left[\frac{1}{\sqrt{x^2 + R^2}}\right]_{0}^{\infty}=\frac{kq\lambda}{R} = \frac{q\lambda}{4\pi\epsilon_0 R}$$
this is the correct answer given in the book. But if we calculate the field due to rod on the ring and then calculate the Force acting on the ring, by Newtons 3rd law we should get the same force
calculating the field due to the rod:
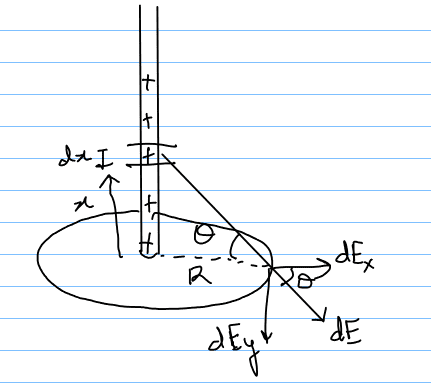
$$|d\vec E| = \frac{k(dq)}{(x^2+R^2)}$$
$$d\vec E = dE_x\hat i + dE_y\hat j$$
$$dE_x = dEcos\theta = \frac{k(dq)}{(x^2 + R^2)}\frac{R}{\sqrt{R^2 + x^2}} = \frac{k\lambda(dx)R}{(R^2+x^2)^{3/2}}$$
$$E_x = k\lambda R\int_{0}^{\infty}\frac{dx}{(R^2 + x^2)^{3/2}}=\frac{k\lambda}{R} = \frac{\lambda}{4\pi\epsilon_0R}$$
$$dE_y = dEsin\theta = k\lambda \frac{x(dx)}{(R^2 + x^2)^{3/2}}$$
$$E_y = k\lambda \int_{0}^{\infty}\frac{x}{(R^2 + x^2)^{3/2}}dx = \frac{k\lambda}{R} = \frac{\lambda}{4\pi\epsilon_0 R}$$
$$\vec E = \frac{\lambda}{4\pi\epsilon_0 R}\hat i + \frac{\lambda}{4\pi\epsilon_0 R}\hat j$$
$$|\vec E| = \frac{\sqrt{2}\lambda}{4\pi\epsilon_0R}$$
The force on the ring due to the field produced by thr rod is hence:
$$F = qE = \frac{\sqrt{2}q\lambda}{4\pi\epsilon_0R}$$
so if my math is correct I just disproved Newtons 3rd law I did the integrals twice by hand and once using wolfram alpha but still haven't been able to catch the error. Can someone help me out. I really hope there is a mistake in the math and not something conceptually wrong.
I did the integrals twice by hand and once using wolfram alpha but still haven't been able to catch the error. Can someone help me out. I really hope there is a mistake in the math and not something conceptually wrong.
The electric field due to the ring is:
$$E = \int\frac{k(dq)}{(\sqrt{R^2 + x^2})^2}\frac{x}{\sqrt{R^2 + x^2}} = \frac{kqx}{(R^2 + x^2)^{3/2}}$$
the force on the rod due to this Electric field produced by the ring is:
Consider a differential element ##dq## of the rod on which the force is:
$$dF = E(dq) = E\lambda(dx)\frac{kqx\lambda(dx)}{(x^2 + R^2)^{3/2}}$$
The total force on the rod by the ring will be:
$$F = kq\lambda\int_{0}^{\infty}\frac{x}{(x^2 + R^2)^{3/2}} dx = -kq\lambda\left[\frac{1}{\sqrt{x^2 + R^2}}\right]_{0}^{\infty}=\frac{kq\lambda}{R} = \frac{q\lambda}{4\pi\epsilon_0 R}$$
this is the correct answer given in the book. But if we calculate the field due to rod on the ring and then calculate the Force acting on the ring, by Newtons 3rd law we should get the same force
calculating the field due to the rod:
$$|d\vec E| = \frac{k(dq)}{(x^2+R^2)}$$
$$d\vec E = dE_x\hat i + dE_y\hat j$$
$$dE_x = dEcos\theta = \frac{k(dq)}{(x^2 + R^2)}\frac{R}{\sqrt{R^2 + x^2}} = \frac{k\lambda(dx)R}{(R^2+x^2)^{3/2}}$$
$$E_x = k\lambda R\int_{0}^{\infty}\frac{dx}{(R^2 + x^2)^{3/2}}=\frac{k\lambda}{R} = \frac{\lambda}{4\pi\epsilon_0R}$$
$$dE_y = dEsin\theta = k\lambda \frac{x(dx)}{(R^2 + x^2)^{3/2}}$$
$$E_y = k\lambda \int_{0}^{\infty}\frac{x}{(R^2 + x^2)^{3/2}}dx = \frac{k\lambda}{R} = \frac{\lambda}{4\pi\epsilon_0 R}$$
$$\vec E = \frac{\lambda}{4\pi\epsilon_0 R}\hat i + \frac{\lambda}{4\pi\epsilon_0 R}\hat j$$
$$|\vec E| = \frac{\sqrt{2}\lambda}{4\pi\epsilon_0R}$$
The force on the ring due to the field produced by thr rod is hence:
$$F = qE = \frac{\sqrt{2}q\lambda}{4\pi\epsilon_0R}$$
so if my math is correct I just disproved Newtons 3rd law
