Abhishekkkk__
- 2
- 0
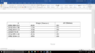
Homework Statement
I need to calculate a spring constant using measurements from a Hooke's Law Apparatus, a spring, and some weights. The weights are hung vertically from the spring and the distance is measured from the equilibrium point of the spring. If I'm solving for k, then k=F/x. I do this for the different lengths of the spring and masses of the weights, and get very different answers for the constant. So here are my questions: 1) Am I even using the right formula? If I'm not, you can go give me the right one. 2) Shouldn't a constant be constant? And help on this matter would be greatly appreciated.