Elbobo
- 145
- 0
(sorry about another topic but this week's HW is hard @_@)
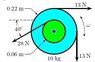
A circular-shaped object has an inner radius
of 6 cm and an outer radius of 22 cm. Three
forces (acting perpendicular to the axis of
rotation) of magnitudes 13 N, 28 N, and 13 N
act on the object, as shown. The force of
magnitude 28 N acts 40◦ below the horizontal.
Find the magnitude of the net torque on
the wheel about the axle through the center
of the object. Answer in units of N · m.
Torque = Fd sin (th)
I ignored the mass because the teacher didn't mention anything about reading over the moment of intertia section in our textbook, but I think she was wrong... Anyway:
Clockwise as the positive direction.
Net Torque = (13 * 0.28) + (13 * 0.28) - (28 * 0.06 sin 40)
Net torque = 6.200116816 m*N (WRONG)
T_T I tried reading the section, but it gave me an equation (Net Torque = Moment of intertia * angular acceleration) I couldn't do anything with, as I didn't know how to solve for the angular acceleration.
Homework Statement
A circular-shaped object has an inner radius
of 6 cm and an outer radius of 22 cm. Three
forces (acting perpendicular to the axis of
rotation) of magnitudes 13 N, 28 N, and 13 N
act on the object, as shown. The force of
magnitude 28 N acts 40◦ below the horizontal.
Find the magnitude of the net torque on
the wheel about the axle through the center
of the object. Answer in units of N · m.
Homework Equations
Torque = Fd sin (th)
The Attempt at a Solution
I ignored the mass because the teacher didn't mention anything about reading over the moment of intertia section in our textbook, but I think she was wrong... Anyway:
Clockwise as the positive direction.
Net Torque = (13 * 0.28) + (13 * 0.28) - (28 * 0.06 sin 40)
Net torque = 6.200116816 m*N (WRONG)
T_T I tried reading the section, but it gave me an equation (Net Torque = Moment of intertia * angular acceleration) I couldn't do anything with, as I didn't know how to solve for the angular acceleration.