How Do You Calculate the Radius of a Pipe in Fluid Mechanics?

AI Thread Summary
To calculate the radius of a pipe in fluid mechanics, the volume flow rate equation Q = πR^4(P1-P2) / 8nL is used, where Q is the flow rate, R is the radius, P1 and P2 are pressures, n is the fluid's viscosity, and L is the length of the pipe. The user initially struggled with the calculation, questioning whether the differential pressure should be interpreted as a height difference or actual pressure. After clarification, it was confirmed that the height difference of 0.045 m can be used to find the pressure difference using the formula ΔP = ρgΔh. The user successfully recalculated the radius after this understanding. The discussion highlights the importance of correctly interpreting variables in fluid mechanics equations.
maos
Messages
4
Reaction score
0

Homework Statement


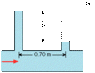
Water (n = 1.00 10-3 Pa·s) is flowing through a horizontal pipe with a volume flow rate of 0.029 m3/s. As the drawing shows, there are two vertical tubes that project from the pipe. From the data in the drawing, find the radius of the horizontal pipe.

11_80.gif


Homework Equations



Q = πR^4(P1-P2) / 8nL


The Attempt at a Solution



0.029 = πR^4(0.045) / (8*10^-3 * .7)

solve for R, multiply by 100. However, i don't get the right answer...


What am i doing wrong? this seems like such a straightforward problem
 

Attachments

  • 11_80.gif
    11_80.gif
    4.3 KB · Views: 509
Physics news on Phys.org
Is the differential pressure, (P1 - P2), in the formula given as the head (height or depth) of water (0.045 m), or is it pressure, in which case \DeltaP = \rhog\Deltah, where \Deltah is the difference in heights of the water columns, i.e. 0.045 m.
 
oh maybe it's pgh. let me give it a second go.
 
yes i got it right. thank you Astronuc for the fast reply! I owe you :)
 

Thread 'Struggling to understand the concept of this question (ice cube in water optics question)'

TL;DR Summary: I came across this question from a Sri Lankan A-level textbook. Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water. I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
View full post »
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Finding height of buffer regions and viscous sublayer turbulent flow
Replies
4
Views
2K
Bernoulli equation / fluid flow / finding height
Replies
6
Views
3K
Oil enters a flexible bend in a pipe -- calculate the force needed to hold the bend in place
Replies
12
Views
1K
Water flow in pipe with two open vertical offshoots
Replies
15
Views
4K
I Shouldn't the pressure difference along a pipe be a negative number?
Replies
8
Views
1K
How Do Viscous Interactions Differ in Vertical and Horizontal Geometries?
Replies
31
Views
3K
Change in gauge pressure using viscous flow through a pipe.
Replies
6
Views
8K
Solve Fluid Mechanics Homework: Q, m, t, P
Replies
4
Views
2K
Velocity of a fluid within a pipe
Replies
5
Views
3K
What is the speed of air flow in a pipe driven by compressed air for 12 minutes?
Replies
24
Views
3K

Hot Threads

Recent Insights

Back
Top