Lapse
- 49
- 4
Homework Statement
[/B]
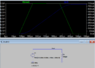
Calculate, and plot along with (on the same plot) the voltage seen below, the current flowing in the following circuit using the integral relationship between the voltage across an inductor and the current through the inductor. Verify your hand calculations and plot using LTspice.
Homework Equations
I = Io+1/L ⋅ ∫Vdτ
The Attempt at a Solution
So I am obviously doing this incorrectly because the current I obtain from solving the integral doesn't match the graph. For example, If I want the current from time 100μs - 200μs:
I = 0 + 1/400μH∫1dτ = 250mA
250mA is too high according to the graph. Where am I going wrong here?