Wale
- 11
- 0
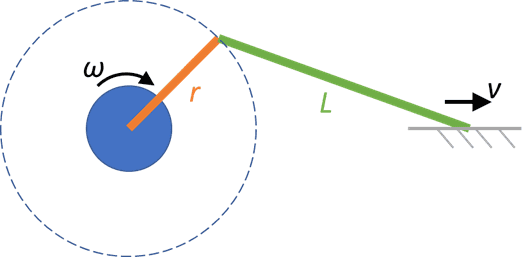
I am trying to design a mechanism which has a hydraulic cylinder driven by a step motor. The motor shaft is connected to the hydraulic cylinder piston via two rods of lengths r and L as shown in the below figure. I want the cylinder's piston to be driven at constant velocity v, so I am trying to solve for the rotational speed profile w (omega) that I need to drive the step motor with in order to achieve the constant linear velocity v.
Any help?
Any help?


