BenBa said:
I see, just from some quick math if the input voltage(absolute value) is less than 150 microVolts it will be between the rails. Noise is approximately on that level, i think its fair to assume for this problem that it hits rail voltage.
OH duh! Push pull amplifiers only amplify current not voltage!
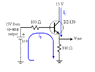
Push-pull amps are great for achieving large output currents, but there will still be an output voltage.
Open loop, only R4 is in the emitter paths of the transistors and the output voltage will be developed across it. You should be able to estimate the output voltage that occurs when the voltage driving the push-pull stage is ± 15V.
I believe they must be asking about the closed loop case, or else it would be trivial. If the feedback fraction is just the reciprocal of the closed-loop gain when open loop gain is very large (which it seems to be) doesn't that mean it does not vary with frequency?
The closed-loop gain will vary with frequency due to the capacitor in the feedback path (But by how much?). It would be helpful to know what effect the capacitor has on the gain over the given frequency range.
This question can be either relatively simple to answer or rather more complicated... you'll have to be the judge based on the material in the course section that this problem comes from.
Unless your text defines some particular conditions for determining the gain of an audio amplifier (input signal voltage and frequency, amplifier load), my suggestion would be to look at the low frequency (f → DC) gain to answer the problem. That would be the simple version.
And how do we find out the closed-loop gain? I know that since the push-pull only amplifies current we are just looking for the gain of the op amp and normally inverting op amps have a gain of -R2/R1 but does this hold when the feedback loop doesn't occur until the all the way after the push-pull amp, and how do we account for the capacitor?
It holds for the whole amplifier, too. The op-amp will drive the push-pull stage with whatever amount of voltage required so that feedback will null the voltage difference between its inputs. Effectively, the push pull stage becomes the new output stage of the op-amp. (you could draw a bigger triangle and include the push-pull stage inside and call that your op-amp!)
The feedback loop is a filter thanks to the capacitor in the path, so the gain will vary with frequency. The only question is by how much? Check to see what effect it will have at either extreme of the signal frequency range (20 Hz - 20 kHz). How does the capacitor impedance compare to R2 for those frequencies?