SUMMARY
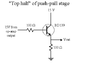
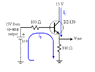
This discussion focuses on analyzing a transistor amplifier circuit, specifically addressing the DC load line for transistor Q1, which is identified as a BD139. The participants clarify that the y-intercept for the load line can be determined using Vcc/R4, where R4 acts as the emitter resistor. Key concepts such as open-loop voltage gain and closed-loop gain are defined, with open-loop referring to the gain without feedback. The conversation emphasizes the importance of understanding the operating point of the transistors in a push-pull configuration, particularly when no input signal is present.
PREREQUISITES
- Understanding of transistor operation, specifically for BJTs like BD139
- Knowledge of DC load line analysis in amplifier circuits
- Familiarity with feedback mechanisms in operational amplifiers
- Basic circuit analysis skills, including the use of Kirchhoff's laws
NEXT STEPS
- Study the characteristics and datasheet of the BD139 transistor
- Learn about DC load line analysis and how to determine operating points
- Explore the concepts of open-loop and closed-loop gain in amplifier circuits
- Investigate the implications of push-pull configurations in amplifier design
USEFUL FOR
Electrical engineering students, circuit designers, and anyone involved in the analysis and design of transistor amplifier circuits will benefit from this discussion.