feistytigger
- 2
- 0
I apologize in advance - I am completely clueless about this one. I thought I had it figured out, but it turns out that I think I don't know where to even start.
Four particles form a square. The charges are q1 = q4 = Q and q2 = q3 = q. What is Q/q if the net electrostatic force on particles 1 and 3 is zero?
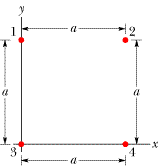
See, I thought it would work out to be 1 since I thought q and Q must be the same for the force to be zero. Apparently I am mistaken. So... show me start to finish pretty please?
Four particles form a square. The charges are q1 = q4 = Q and q2 = q3 = q. What is Q/q if the net electrostatic force on particles 1 and 3 is zero?
See, I thought it would work out to be 1 since I thought q and Q must be the same for the force to be zero. Apparently I am mistaken. So... show me start to finish pretty please?