Oscillation of a vertical spring

[CAF123]

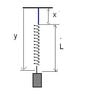
The natural length is not -a. It is a and always positive - simply because it is a length. What you meant to say was the position of the bottom end at the natural length was -a, which is quite a mouthful.

The fallacy of your argument is this assumption: "I know that if the mass goes down by -x then the top end of the spring goes down by -x." The top and the bottom ends are obviously connected by the spring, but you can't assume one simply repeats the motion of the other. This is obvious when you consider the fixed top: the bottom can be at pretty much any position x, despite the fixed top's being, well, fixed.

The mass will undergo a greater displacement -c sin(nt). So I should have -k(-x - c sin(nt) +a) with l = z-x => -k(l-z -csin(nt) + a) => -k(l-(-csin(nt))-csin(nt) + a) = -k(l+a).
EDIT:No, this is still not right...but I cannot see where.
EDIT2: Actually, I think I have it. In my above setup, I should have -l = -x -(-z) = -x + z. So from -k(-x - csin(nt) + a), I have -k(-l-z - csin(nt) + a) = -k(-l - (-csin(nt)) - csin(nt) + a) = -k(-l + a), which I think is the same as what we got a few posts above in the discussion.

 

[voko]

You seem stuck on the idea that you can equate the motion of end end with that of the other. But that is not true. All you know is the motion of the top end, the motion of the bottom end is unknown. They are connected indirectly, via the force and acceleration.

 

[CAF123]

The bottom motion is connected to the top motion by expressing l in terms of z and x. (see my EDIT2 in my last post), thanks.
EDIT: I thought this fixed things but it messes the LHS up now. I think I was along the right lines in post 11, but I just can't seem to fix the negative signs.

 

[CAF123]

Okay let me try from scratch:

Consider the spring end to be at a distance -a. Now consider some displacement of the bottom end to -x. This means from the springs natural length, it has extended a distance
(-x +a). But there is also some displacement at the top end by -z. I believe these are related by the length of the spring: (-x + a) + z = l, so x = z + a -l.

Since the extension of the spring is (-x +a) this gives (l-z) (using x from above) and so the displacement of the bottom end is -k(l-z + a)

Writing the eqn of motion for the mass on the spring: $m\ddot{x} = -k(l-z+a) -mg$. I haven't assumed anything about the displacement of the bottom mass here (only that z and x are related through l) but I still get a wrong sign and a stray z term. I don't see where I am going wrong.

 

[ehild]

See picture. The ceiling is the zero of coordinate y and downward is the positive direction. The top of the spring is at x=csin(nt). The length of the spring is L. so y=x+L.

For he mass m, m\ddot {y}=mg-k(L-a)\rightarrow \ddot {x} +\ddot L =g-\frac{k}{m}(L-a)

The relaxed length of the spring is a. When the hanged mass is rest, the length is b, so mg=k(b-a), as you have shown. The natural frequency is ω. ω²=√(k/m). So g=ω²(b-a).

Find the second derivative of x. Also substitute ω² for k/m and ω²(b-a) for g.

ehild

Edit: The zero of y is not at the ceiling but at the point the upper end of the spring oscillates about.

 

[CAF123]

See picture. The ceiling is the zero of coordinate y and downward is the positive direction. The top of the spring is at x=csin(nt). The length of the spring is L. so y=x+L.

For he mass m, m\ddot {y}=mg-k(L-a)\rightarrow \ddot {x} +\ddot L =g-\frac{k}{m}(L-a)

If downwards is positive, shouldn't that be -(-k(L-a))? So this means that L is the extension of the spring from a. This is clear from your diagram.

Many thanks.
Where was it that I was going wrong? Was I too concentrated with the displacement of the bottom mass?

 

[voko]

Consider the spring end to be at a distance -a. Now consider some displacement of the bottom end to -x. This means from the springs natural length, it has extended a distance
(-x +a). But there is also some displacement at the top end by -z. I believe these are related by the length of the spring: (-x + a) + z = l, so x = z + a -l.

The relation between x and z, if downward is negative, is L = z - x. The extension from the natural length is X = -(L - a). The restoring force (at the bottom) is -kX = k(L - a).

 

[ehild]

If downwards is positive, shouldn't that be -(-k(L-a))? So this means that L is the extension of the spring from a. This is clear from your diagram.

L is the legth of the spring. a is the unstretched length . The change of length is L-a>0. The spring force points upward, so it is -k(L-a), opposite to mg.

Well, the zero is a bit deeper then the ceiling, so the upper part of the spring can move about it.

Many thanks.
Where was it that I was going wrong? Was I too concentrated with the displacement of the bottom mass?

I don not quite follow your notations. If you can attach a sketch... Choose a fixed point and give all positions with respect to that point.

ehild

 

[CAF123]

I understand where I went wrong now - The question says we have a displacement at the top end and somehow I simply neglected that and drew a sketch with the mass at the end displaced instead. Thank you voko and ehild.

I now need to find the particular solution to this eqn. From the words of the question, should I let the initial conditions be $L(0) = a$ and $\dot{L}(0) = nc$?

My method was to split up and solve two eqns:
1): Solve $\ddot{L} + \omega^2 L = \omega^2b \Rightarrow L =b$by inspection.
2): Solve $\ddot{L} + \omega^2L = cn^2 \sin(nt)$
I found a solution of $L = \frac{cn^2}{\omega^2 - n^2} \sin(nt)$

Putting these together:
General solution to inhomogeneous eqn: General soln to homogeneous eqn + Particular solution to inhomogeneous.
So I get $$L(t) = A \cos (\omega t) + B \sin(\omega t) + b + \frac{cn^2}{\omega^2 - n^2}$$ A and B can be determined by the Initial conditions, but I want to check they are correct before I start.
Thanks.

 

[ehild]

The sin(nt) factor is missing from the final expression.

L(t) = A \cos (\omega t) + B \sin(\omega t) + b + \frac{cn^2}{\omega^2 - n^2} \sin(nt).

Good job!

ehild

 

[CAF123]

The sin(nt) factor is missing from the final expression.

L(t) = A \cos (\omega t) + B \sin(\omega t) + b + \frac{cn^2}{\omega^2 - n^2} \sin(nt).

Good job!

ehild

Thanks. Are the IC correct?

 

[ehild]

There are no initial conditions specified. The formula for L(t) is the general solution if ω≠n. You can fit any initial condition to it.
There is one problem left: what happens if ω=n.

ehild

 

[CAF123]

There are no initial conditions specified. The formula for L(t) is the general solution if ω≠n. You can fit any initial condition to it.
There is one problem left: what happens if ω=n.

ehild

I have the question
4) 'Write down the initial conditions based on the description above (that is the the problem statement) and find L(t).'

I must be able to make some sort of IC from the fact it is moving downwards at t=0, no?

Also if $\omega = n$then the last term blows up. So the displacement of the top end is in sinc with that of the natural freq of the spring. Hence if this is the case, is it right to say that we can reach infinite displacements of the spring? (I.e the resonance)

 

[voko]

I have the question
4) 'Write down the initial conditions based on the description above (that is the the problem statement) and find L(t).'

I must be able to make some sort of IC from the fact it is moving downwards at t=0, no?

You used this assumption when deciding what sign you should have in front of c sin nt. At this stage you have to assume that x(0) = 0 and x'(0) = 0 and derive the conditions for L from that.

Also if $\omega = n$then the last term blows up. So the displacement of the top end is in sinc with that of the natural freq of the spring. Hence if this is the case, is it right to say that we can reach infinite displacements of the spring? (I.e the resonance)

What happens is that the solution is no longer valid. You need to find a solution that is valid in this case.

 

[CAF123]

Assuming at t=0 that x(0) =0 and x'(0)=0 would mean that L(0)=a and L'(0) = 0 right? (where x is the displacement of the top end of the spring).

In the case of omega =n, I have:$$L(t) = A \cos (\omega t) + B \sin (\omega t) + b - \frac{c \omega^2}{2 \omega}t\cos (\omega t)$$

What I was trying to say in my last post about the case omega =n was that physically, we can get in theory, infinite amplitude. (I think)

 

[ehild]

"The top of the spring moving downwards at t=0" means that c is positive if the positive direction is downward. You solved a differential equation for L(t). You can use any initial condition, concerning L.. As an example, it can be that initially the spring is stretched by some length d from its original length and released (so dL/dt =0 and L=a+d.) Or the length of the spring is b at t=0 and dL/dt=0.

If ω=n a particular solution is L=-(0.5cn )t cos(nt) + b. Try.

ehild

 

[CAF123]

"The top of the spring moving downwards at t=0" means that c is positive if the positive direction is downward. You solved a differential equation for L(t). You can use any initial condition, concerning L.. As an example, it can be that initially the spring is stretched by some length d from its original length and released (so dL/dt =0 and L=a+d.) Or the length of the spring is b at t=0 and dL/dt=0.

So, L(0) = a and L'(0) = 0?

If ω=n a particular solution is L=-(0.5cn )t cos(nt) + b. Try.

See my last post

 

[ehild]

So, L(0) = a and L'(0) = 0?

That is also a possible choice for initial conditions. Do not forget that you have a differential equation for L, length of the spring. The motion of the top is given.

I haven't seen your last post before sending my one. OK , that is the solution when ω=n.


ehild

 

[CAF123]

That is also a possible choice for initial conditions. Do not forget that you have a differential equation for L, length of the spring. The motion of the top is given.

Actually I reread the question. It explicitly says '...moving downwards at t=0' so does this not imply that the spring may be stretched? ( and if so, L(0) = a would not hold)

 

[ehild]

The top of the spring is moving downwards according to the function csin(nt). At t =0 the displacement of the top is zero. The whole spring is below its top, is'nt it? And a mass is attached to the bottom end. Initially you can do something with that mass, lift up, pull down, or giving it some velocity. So the spring can be stretched initially, but can be unstretched. Or it can be even compressed.

ehild

 

[voko]

L = z - x = - c sin nt - x.
L' = - cn cos nt - x'

if x(0) = x'(0) = 0, what are L(0) and L'(0)?

 

[CAF123]

L = z - x = - c sin nt - x.
L' = - cn cos nt - x'

if x(0) = x'(0) = 0, what are L(0) and L'(0)?

Would that give L(0)=0 and L'(0)=-cn?
L(0) being 0 at t=0 does not make much sense to me since the spring is always going to have its natural length.

 

[ehild]

'Write down the initial conditions based on the description above (that is the the problem statement) and find L(t).'

A mass m hangs in equilibrium at the lower end of a vertical spring of natural length a, extending the spring to be a length b.

In case of initial setup that the hanging mass is in equilibrium before the top of the spring starts to oscillate, the initial conditions are L(0)=b and L'(0)=0.

ehild

Edit: I meant y'=0, so L'(0)=-cn.

 

[voko]

Would that give L(0)=0 and L'(0)=-cn?
L(0) being 0 at t=0 does not make much sense to me since the spring is always going to have its natural length.

You are right, x(0) is not zero. At t = 0 the system is in equilibrium.

 

[CAF123]

You are right, x(0) is not zero. At t = 0 the system is in equilibrium.

So L(0) = b if the system is in equilibrium and L'(0) = -cn?

 

[voko]

That is how I interpret the formulation:

"A mass m hangs in equilibrium at the lower end of a vertical spring of natural length a, extending the spring to be a length b."

That means x(0) = -b, x'(0) = 0.

"2) The top end of the spring is made to oscillate vertically with a displacement csin(nt), moving downwards at t=0."

The conditions on the length follow directly from the given law of the top end's motion and the equilibrium condition on the bottom end. "Moving downward" here states explicitly that the top end is moving at t = 0, which in conjunction with x'(0) = 0 can only mean that the length is changing at t = 0.

 

[ehild]

So L(0) = b if the system is in equilibrium and L'(0) = -cn?

That looks correct.

ehild

 

[CAF123]

That looks correct.

ehild

Okay, the only thing I don't understand now is that in the question it says the top end is moving downwards at t=0. So wouldn't that move the whole system out of equilibrium?
Thanks.

 

[voko]

Okay, the only thing I don't understand now is that in the question it says the top end is moving downwards at t=0. So wouldn't that move the whole system out of equilibrium?
Thanks.

The mass, not the entire system, is said to be in equilibrium. Even though that still sounds a little fishy.

The trouble that you have with grasping the behavior is due to a tiny bit of unrealism in the system: it is not possible to make the top end move in STRICT accordance with c sin nt and at the same time have x'(0) = 0. The sine extends infinitely back in time, so there must have been some oscillations in the past to have the motion in the form c sin nt and to be able to take its derivative. And if there were some oscillations, we can't assume x'(0) = 0. If there were none, the law of motion is not sinusoidal, and z'(0) may not even exist.

 

[ehild]

Okay, the only thing I don't understand now is that in the question it says the top end is moving downwards at t=0. So wouldn't that move the whole system out of equilibrium?
Thanks.

Imagine you have a motor attached to the top of the spring which makes the top end moving. Before starting the motor the mass is in equilibrium, y=b and y'=0. As you switch the motor on, the displacement of the top end is still zero, but its velocity is -cn. So L(0)=b and L'(0)=-cn.

Initially the hanging mass does not "feel" anything, as the spring force is still k(b-a), and it is in equilibrium with gravity.

As time proceeds, the spring gets shorter, the spring force decreases, so the mass starts to descend.

ehild