etf
- 179
- 2
Hi!
1. Homework Statement
My task is to calculate amplitude and phase spectrum of this signal:
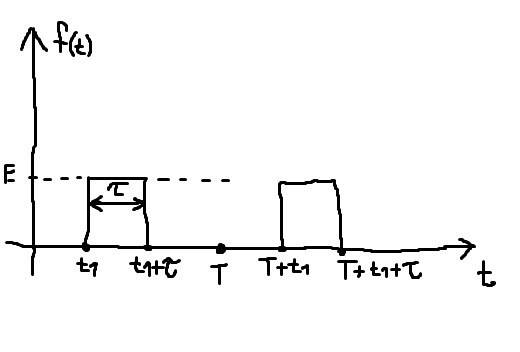
My idea is to calculate complex Fourier series of this signal, $$f(t)=\sum_{n=-\infty}^{n=+\infty}Fne^{j\frac{2n\pi t}{T}},$$ where $$Fn=\frac{1}{T}\int_{0}^{T}f(t)e^{-j\frac{2n\pi t}{T}}. $$Fn will be some complex number, which can be written as $$|Fn|e^{j\Theta n},$$ where $$|Fn|$$ is amplitude spectrum and $$\Theta n$$ is phase spectrum.
I got $$Fn=\frac{E\tau }{T}\frac{\sin{(nw0\tau /2)}}{nw0\tau /2}e^{-jnw0(t1+\tau /2)}, $$ where w0=2*pi/T. We see that phase spectrum is $$\Theta n=-nw0(t1+\tau /2)$$ and amplitude spectrum is $$|Fn|=\frac{E\tau }{T}\frac{\sin{(nw0\tau /2)}}{nw0\tau /2}.$$ Now for some values of $$\tau, $$ $$E$$ and $$T$$ I can plot amplitude and phase spectrum as function of n?
[/B]
1. Homework Statement
My task is to calculate amplitude and phase spectrum of this signal:
Homework Equations
My idea is to calculate complex Fourier series of this signal, $$f(t)=\sum_{n=-\infty}^{n=+\infty}Fne^{j\frac{2n\pi t}{T}},$$ where $$Fn=\frac{1}{T}\int_{0}^{T}f(t)e^{-j\frac{2n\pi t}{T}}. $$Fn will be some complex number, which can be written as $$|Fn|e^{j\Theta n},$$ where $$|Fn|$$ is amplitude spectrum and $$\Theta n$$ is phase spectrum.
The Attempt at a Solution
I got $$Fn=\frac{E\tau }{T}\frac{\sin{(nw0\tau /2)}}{nw0\tau /2}e^{-jnw0(t1+\tau /2)}, $$ where w0=2*pi/T. We see that phase spectrum is $$\Theta n=-nw0(t1+\tau /2)$$ and amplitude spectrum is $$|Fn|=\frac{E\tau }{T}\frac{\sin{(nw0\tau /2)}}{nw0\tau /2}.$$ Now for some values of $$\tau, $$ $$E$$ and $$T$$ I can plot amplitude and phase spectrum as function of n?
[/B]
Last edited: