erik006
- 5
- 0
Note: This is a question about a physics experiment. As such, it does not completely fit into the provided template, but I'll do my best to stick to it anyway.
The problem is about an experiment about parallel plates capacitors. The experimental setup is the following:
The full description of the lab can be found here: http://epic.mcmaster.ca/%7Eglen/2a3/2a4_exp3.pdf, if you're interested.
I have several questions about this:
firstly, there is a derivation in the lab manual of the capacitance with respect to the rate of change of voltage with respect to time:
C = \frac{Q}{V}
Q = C
\Delta Q = C\Delta V
\frac{\Delta Q}{\Delta T} = C * \frac{\Delta V}{\Delta T}
but,
\frac{\Delta Q}{\Delta T} = I
so we know that the V/T is inversely proportional to the capacitance.
Question 1: re-arranging the equations leads me to believe this constant of proportionality is I, is that correct?
I can use the following equation to calculate the theoretical capacitance of the plates:
C = \frac{\epsilon A}{d}
Where A is the area of one of the plates (same as the other), \delta is the permittivity of free space (~air), and d is the distance between the plates.
So I calculated the theoretical capacitance & the capacitance from my measurements. I then proceeded to graph them:
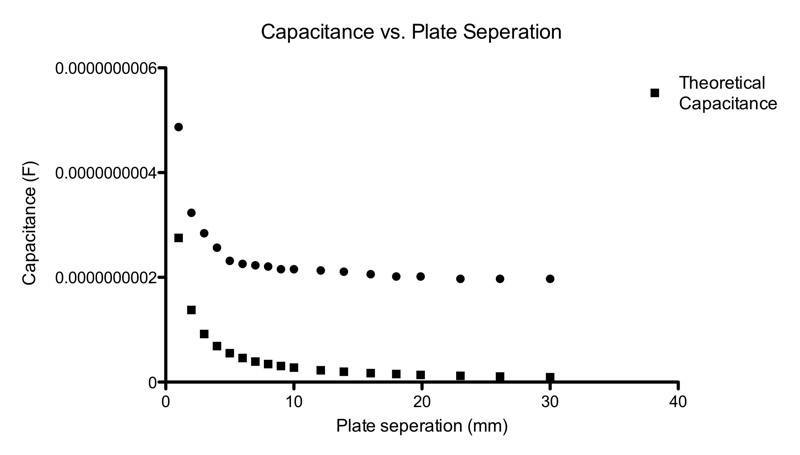
Obviously there's a bias error that is affecting my results.
It seems to me that there are several things affecting these results, some of which I'm not sure what the exact effect of them is:
Question 2: It is unclear to me how exactly reactance & inductive loading tie into this DC current, I've only learned about reactance, impedance, etc in an AC context, could someone enlighten me?
Question 3: Is my approach correct? Any further hints?
Kind regards,
Erik
Homework Statement
The problem is about an experiment about parallel plates capacitors. The experimental setup is the following:
- Two round parallel plates with a radius = 0.0999 m.
- a constant current provided with magnitude 30uA
- The plates are charged and discharged at a circuit frequency of 20Khz using a solid-state switch
- -The resultant charging waveform is observed on an oscilloscope, and the potential difference between the bottom of the waveform and the top is recorded
The full description of the lab can be found here: http://epic.mcmaster.ca/%7Eglen/2a3/2a4_exp3.pdf, if you're interested.
I have several questions about this:
firstly, there is a derivation in the lab manual of the capacitance with respect to the rate of change of voltage with respect to time:
C = \frac{Q}{V}
Q = C
\Delta Q = C\Delta V
\frac{\Delta Q}{\Delta T} = C * \frac{\Delta V}{\Delta T}
but,
\frac{\Delta Q}{\Delta T} = I
so we know that the V/T is inversely proportional to the capacitance.
Question 1: re-arranging the equations leads me to believe this constant of proportionality is I, is that correct?
I can use the following equation to calculate the theoretical capacitance of the plates:
C = \frac{\epsilon A}{d}
Where A is the area of one of the plates (same as the other), \delta is the permittivity of free space (~air), and d is the distance between the plates.
So I calculated the theoretical capacitance & the capacitance from my measurements. I then proceeded to graph them:
Obviously there's a bias error that is affecting my results.
It seems to me that there are several things affecting these results, some of which I'm not sure what the exact effect of them is:
- The oscilliscope introduces resistive, capacitive and inductive loading
- the rest of the circuit has a small capacitance
- the frequency of the waveform (due to the current switching) leads to reactance (it will resist the change in voltage)?
Question 2: It is unclear to me how exactly reactance & inductive loading tie into this DC current, I've only learned about reactance, impedance, etc in an AC context, could someone enlighten me?
Question 3: Is my approach correct? Any further hints?
Kind regards,
Erik
Attachments
Last edited:
