ncm2
- 14
- 0
Homework Statement
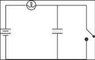
Initially the switch is closed in the circuit shown and the light bulb is shining brightly. What happens when the switch is opened? (diagram in attached link)
1. The bulb goes out immediately.
2. The bulb gets gradually brighter.
3. The bulb gets gradually dimmer.
4. It cannot be determined.
5. The bulb continues to shine without a change in brightness.
Homework Equations
Vc=Vo*exp(-t/RC)
The Attempt at a Solution
I believe that the capacitor should cause the light to gradually dim. However, I also think that the open switch should mean no current flow, which would mean the bulb would immediately go out.
Any explanation is much appreciated