dtesselstrom
- 29
- 0
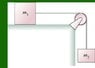
Blocks of mass m1 and m2 are connected by a massless string that passes over the pulley in the figure. The pulley turns on frictionless bearings, and mass m1 slides on a horizontal, frictionless surface. Mass m2 is released while the blocks are at rest.
Suppose the pulley has mass mp and radius R. Find the acceleration of m1.
Find the tension in the upper portion of the string.
Find the tension in the lower portions of the string.
Ive tried R*g*m2/(1/2*mp*r^2)*R and it said it needs mass1 in the problem but I couldn't figure out where it is needed
Suppose the pulley has mass mp and radius R. Find the acceleration of m1.
Find the tension in the upper portion of the string.
Find the tension in the lower portions of the string.
Ive tried R*g*m2/(1/2*mp*r^2)*R and it said it needs mass1 in the problem but I couldn't figure out where it is needed